Cho hình lăng trụ lục giác đều ABCDEF.A’B’C’D’E’F’ có cạnh đáy bằng a, chiều cao bằng h.
LG 1
Tính diện tích xung quanh và thể tích hình trụ ngoại tiếp hình lăng trụ.
Lời giải chi tiết:
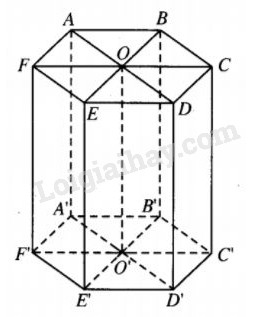
Hình trụ ngoại tiếp hình lăng trụ đã cho có trục là OO’ (O, O’ là tâm hai đáy của hình lăng trụ) và đường tròn đáy của hình trụ này là đường tròn ngoại tiếp đáy của hình lăng trụ.
Dễ thấy bán kính đường tròn đáy của hình trụ ngoại tiếp bằng a.
Vậy diện tích xung quanh của hình trụ đó là \({S_1} = 2\pi ah,\) thể tích khối trụ đó là \({V_1} = \pi {a^2}h.\)
LG 2
Tính diện tích toàn phần và thể tích hình trụ nội tiếp hình lăng trụ.
Lời giải chi tiết:
Hình trụ nội tiếp hình lăng trụ đã cho có trục là OO’, đường tròn đáy của hình trụ này là đường tròn nội tiếp đáy hình lăng trụ.
Dễ thấy bán kính đường tròn đáy của hình trụ nội tiếp bằng \({{a\sqrt 3 } \over 2}\).
Vậy diện tích toàn phần của hình trụ đó là
\({S_2} = 2\pi {{a\sqrt 3 } \over 2}.h + 2\pi {\left( {{{a\sqrt 3 } \over 2}} \right)^2} = \pi a\sqrt 3 \left( {h + {{\sqrt 3 } \over 2}a} \right),\)
Thể tích hình trụ đó là
\({V_2} = \pi {\left( {{{a\sqrt 3 } \over 2}} \right)^2}.h = {3 \over 4}\pi {a^2}h.\)
soanvan.me
