Xét hình trụ nội tiếp một mặt cầu bán kính R mà diện tích thiết diện qua trục hình trụ là lớn nhất. Tính :
LG 1
Thể tích V và diện tích toàn phần \({S_{tp}}\) của hình trụ.
Lời giải chi tiết:
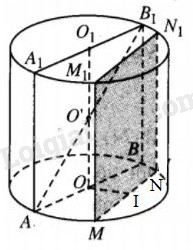
Gọi O’ là trung điểm của trục \({O_1}O\) của hình trụ thì O’ là tâm mặt cầu đã cho. Kí hiệu h và r lần lượt là chiều cao và bán kính đáy của hình trụ thì diện tích thiết diện qua trục là \({S_{td}} = 2r.h.\)
Mặt khác \({R^2} = O'{A^2} = {r^2} + {{{h^2}} \over 4} \Rightarrow {r^2} = {R^2} - {{{h^2}} \over 4}.\)
Từ đó \({S_{td}} = h\sqrt {4{R^2} - {h^2}} = \sqrt {{h^2}(4{R^2} - {h^2})} .\)
Vậy \({S_{td}}\) lớn nhất khi và chỉ khi \(h = R\sqrt 2 .\)
Khi đó \(r = \sqrt {{R^2} - {1 \over 4}.2{R^2}} = {{R\sqrt 2 } \over 2} = {h \over 2},\) tức là thiết diện qua trục là hình vuông.
\(V = \pi {r^2}h = 2\pi {r^2}.r = 2\pi {r^3} = {{\pi {R^3}\sqrt 2 } \over 2}.\)
\({S_{tp}} = 2\pi {r^2} + 2\pi rh = 3\pi {R^2}.\)
LG 2
Thể tích hình lăng trụ n-giác đều nội tiếp hình trụ và thể tích hình lăng trụ n-giác đều ngoại tiếp hình trụ.
Lời giải chi tiết:
\( \bullet \) Dễ thấy diện tích đáy của hình lăng trụ n-giác đều nội tiếp hình trụ là \({n \over 2}{r^2}\sin {{2\pi } \over n}\).
Vậy thể tích hình lăng trụ đó là:
\(V_{\text{lăng trụ}}={n \over 2}{r^2}\sin {{2\pi } \over n}.2r = n{r^3}\sin {{2\pi } \over n} \)
\(= {{n{R^3}} \over {2\sqrt 2 }}\sin {{2\pi } \over n}\)
\( \bullet \) Xét đa giác đều n cạnh ngoại tiếp đường tròn đáy hình trụ thì độ dài cạnh của đa giác bằng \(2r\tan {\pi \over n},\) từ đó diện tích đáy hình trụ là
\({S_{đáy}} = n.{1 \over 2}2r.\tan {\pi \over n}.r = n{r^2}\tan {\pi \over n}.\)
Vậy thể tích hình lăng trụ n-giác đều ngoại tiếp hình trụ là
\(n{r^2}\tan {\pi \over n} \cdot 2r = 2n{r^3}.\tan {\pi \over n} \)
\(= {{n{R^3}} \over {\sqrt 2 }}\tan {\pi \over n}\)
LG 3
Diện tích thiết diện của hình trụ khi cắt bởi một mặt phẳng song song với trục hình trụ và cách trục một khoảng \({R \over 2}.\)
Lời giải chi tiết:
Giả sử thiết diện là \(MN{N_1}{M_1}\) thì \(MN{N_1}{M_1}\) là hình chữ nhật. Gọi I là trung điểm của MN thì
\(OI = {R \over 2}\) và \(IM = \sqrt {{r^2} - {{{R^2}} \over 4}} = \sqrt {{{{R^2}} \over 2} - {{{R^2}} \over 4}} = {R \over 2}.\)
Vậy diện tích thiết diện \(MN{N_1}{M_1}\) là
\(MN.N{N_1} = 2IM.h = R.R\sqrt 2 = {R^2}\sqrt 2 .\)
soanvan.me
