Đề bài
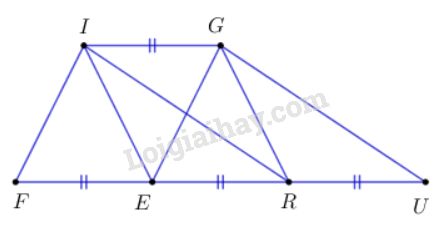
Xem hình \(142\) (\(IG// FU\)). Hãy đọc tên một số hình có cùng diện tích với hình bình hành \(FIGE.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Diện tích hình bình hành bằng tích của một cạnh với chiều cao ứng với cạnh đó.
\(S = ah\)
- Diện tích tam giác có cạnh \(a\), chiều cao tương ứng \(h\) là \(S = \dfrac{1}{2}ah\)
Lời giải chi tiết
Gọi \(h\) là chiều cao từ \(I\) đến \(FE\) thì \(h\) cũng là chiều cao từ \(I\) đến \(FU\)
+) Nhận thấy \(FIGE, IGRE, IGUR\) là các hình bình hành (do có 1 cặp cạnh song song và bằng nhau)
Nên ta có:
\({S_{FIGE}} =h.FE\), \({S_{IGRE}} =h.RE\), \({S_{IGUR}}=h.RU\)
Mà \(FE = ER = RU\)
Nên \({S_{FIGE}} = {S_{IGRE}} = {S_{IGUR}}\) \(( = h. FE)\)
+) Ta có \(FR= EU=2FE\) nên:
\({S_{IFR}}= \dfrac{1}{2}h.FR= \dfrac{1}{2}.h.2.FE = h.FE\)
\({S_{GEU}} =\dfrac{1}{2}h.EU= \dfrac{1}{2}.h.2.FE = h.FE\)
\( \Rightarrow {S_{IFR}} = {S_{GEU}} = {S_{FIGE}}\) \((=h.FE)\)
Vậy \({S_{FIGE}} = {S_{IGRE}} = {S_{IGUR}}\)\(\, = {S_{IFR}} = {S_{GEU}}\)
