Đề bài
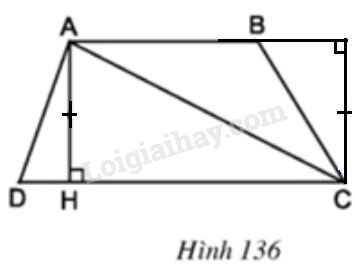
Hãy chia hình thang \(ABCD\) thành hai tam giác rồi tính diện tích hình thang theo hai đáy và đường cao (h.\(136\)).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính diện tích tam giác:
\(S = \dfrac{1}{2}ah\)
\(S\) là diện tích tam giác.
\(a\) là cạnh của tam giác.
\(h\) là chiều cao ứng với cạnh \(a\) của tam giác.
Lời giải chi tiết
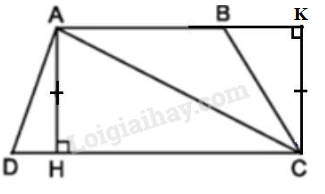
Kẻ \(CK \bot AB\) tại \(K\).
Vì \(AH\bot CD\) mà \(AB//CD\) nên \(AH\bot AB\)
Ta có: \(AB//CD\) (do ABCD là hình thang) và \(AH//CK\) (do cùng vuông với AB) nên \(AHCK \) là hình bình hành.
Suy ra \(AH=CK\) (tính chất)
\({S_{ADC}} = \dfrac{1}{2}AH.DC\)
\({S_{ABC}} = \dfrac{1}{2}CK.AB=\dfrac{1}{2}AH.AB\)
Suy ra: \({S_{ABCD}} = {S_{ABC}} + {S_{ADC}}\)\(\, = \dfrac{1}{2}AH.AB + \dfrac{1}{2}AH.DC \)\(\,= \dfrac{1}{2}AH.(AB + DC)\)
soanvan.me