Đề bài
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số
\(y = -2x\) ; (1)
\(y = 0,5x\) ; (2)
b) Qua điểm K(0;2) vẽ đường thẳng (d) song song với trục Ox. Đường thẳng (d) cắt các đường thẳng (1) , (2) lần lượt tại A, B. Tìm tọa độ của các điểm A, B.
c) Hãy chứng tỏ rằng \(\widehat {AOB} = {90^0}\) (hai đường thẳng \(y = -2x\) và \(y = 0,5x\) vuông góc với nhau).
Phương pháp giải - Xem chi tiết
Cách vẽ đồ thị hàm số \(y = ax + b\) \((a \ne 0)\)
+ Nếu \(b = 0\) ta có hàm số \(y = ax\). Đồ thị của \(y = ax\) là đường thẳng đi qua gốc tọa độ \(O(0;0)\) và điểm \(A(1;a)\);
+ Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b)\); \(B( - \dfrac{b}{a};0)\).
Sử dụng tam giác đồng dạng để chứng minh hai đường thẳng vuông góc.
Lời giải chi tiết
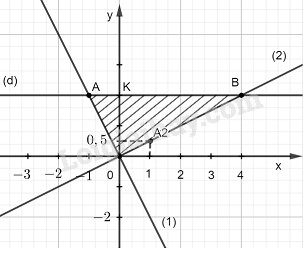
a) * Vẽ đồ thị hàm số \(y = -2x\)
Cho \(x = 0\) thì \(y = 0.\) Ta có: \(O(0;0)\)
Cho \(x = -1\) thì \(y = 2.\) Ta có : \(A(-1;2)\)
Đồ thị hàm số \(y = -2x\) là đường thẳng đi qua điểm O và A.
* Vẽ đồ thị hàm số \(y = 0,5 x\)
Cho \(x = 0\) thì \(y = 0.\) Ta có : \(O(0;0)\)
Cho \(x = 1\) thì \(y = 0,5\) . Ta có: \(A_2(1;0,5)\)
Đồ thị hàm số \(y = 0,5x\) đi qua O và \(A_2.\)
b) Đường thẳng (d) song song với trục Ox và đi qua điểm \(K(0;2)\) nên nó là đường thẳng \(y = 2\)
Đường thẳng \(y = 2\) cắt đường thẳng (1) tại A nên điểm A có tung độ bằng \(2\).
Thay \(y = 2\) vào phương trình \(y = -2x\) ta được \(2=-2x\Rightarrow x = -1.\)
Vậy điểm \(A(-1;2)\)
Đường thẳng \(y = 2\) cắt đường thẳng (2) tại B nên điểm B có tung độ bằng 2.
Thay \(y = 2\) vào phương trình \(y = 0,5x\) ta được \(2=0,5x \Rightarrow x = 4\)
Vậy điểm \(B(4;2)\).
c) Xét hai tam giác vuông \(OAK\) và \(BOK\) , ta có:
\(\eqalign{
& \widehat {OKA} = \widehat {OKB} = {90^0} \cr
& \dfrac{{AK}}{{OK}} = {1 \over 2};{{OK} \over {KB}} = {2 \over 4} = {1 \over 2} \cr
& \Rightarrow {{AK} \over {OK}} = {{OK} \over {KB}} \cr} \)
Suy ra \(\Delta OAK\) đồng dạng với \(\Delta BOK\)
Suy ra: \(\widehat {KOA} = \widehat {KBO}\)
Mà \(\widehat {KBO} + \widehat {KOB} = {90^0}\) (do tam giác KOB vuông tại K)
Suy ra: \(\widehat {KOB} + \widehat {KOA} = {90^0}\) hay \(\widehat {AOB} = {90^0}\).
Hay hai đường thẳng \(y = -2x\) và \(y = 0,5x\) vuông góc với nhau.
soanvan.me
