Đề bài
Cho đường tròn \((O)\) đường kính \(6cm,\) dây \(AB\) bằng \(2cm.\) Khoảng cách từ \(O\) đến \(AB\) bằng:
\((A)\) \(\sqrt {35} cm\) ; \((B)\) \(\sqrt 5 cm\) ;
\((C)\) \(4\sqrt 2 cm\) ; \((D)\) \(2\sqrt 2 cm\).
Hãy chọn phương án đúng.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức:
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Sử dụng định lí Py-ta-go: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết
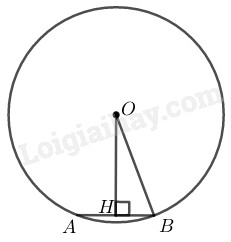
Ta có: \(OA=OB=6:2=3cm\)
Kẻ \(OH \bot AB\) tại \(H\) mà OH là 1 phần đường kính và AB là dây cung của đường tròn tâm O
\(\Rightarrow AH=HB=\dfrac{1}{2}AB=1cm\) (quan hệ giữa đường kính và dây)
Xét trong \(\Delta OHB,\) có:
\(OB^2=OH^2+HB^2\) (định lý Pytago)
\(\Rightarrow OH^2=OB^2-HB^2\)
\(OH^2=3^2-1^2=8\)
\(\Rightarrow OH=2\sqrt{2}\)
Vậy chọn \((D).\)
soanvan.me
