Đề bài
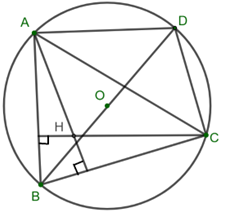
Cho đường tròn tâm O và dây cung BC không đi qua O. Điểm A chuyển động trên cung lớn BC của đường tròn sao cho tam giác ABC nhọn. Gọi H là trực tâm của tam giác ABC. Chứng minh rằng \(\overrightarrow {AH} \) có độ dài không đổi.
Phương pháp giải - Xem chi tiết
Chứng minh AH không đổi
Bước 1: Kẻ đường kính BD của đường tròn (O)
Bước 2: Chứng minh ADCH là hình bình hành (dấu hiệu tứ giác có các cặp cạnh song song)
Bước 3: Từ giả thiết bước 2 suy ra AH = DC rồi kết luận
Lời giải chi tiết
Kẻ đường kính BD của đường tròn (O)
Ta có:
\(\widehat {BAD}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {BAD}\) = 900 \( \Rightarrow AD \bot AB\) (1)
Mặt khác, \(CH \bot AB\) (giả thiết) (2)
Từ (1) và (2) suy ra AD // CH (3)
Chứng minh tương tự ta được AH // CD (4)
Từ (3) và (4) suy ra ADCH là hình bình hành \( \Rightarrow \)AH = DC
Mà DC không đổi nên AH không đổi
\( \Rightarrow \)\(\overrightarrow {AH} \) có độ dài không đổi
