Đề bài
Cho hình thang \(ABCD (AB//CD)\). Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\).
a) Chứng minh rằng \(OA.OD = OB.OC\).
b) Đường thẳng qua \(O\) vuông góc với \(AB\) và \(CD\) theo thứ tự tại \(H\) và \(K\).
Chứng minh rằng \(\dfrac{OH}{OK} = \dfrac{AB}{CD}\)
Phương pháp giải - Xem chi tiết
Áp dụng
- Định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
- Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đô đồng dạng
- Tính chất hai tam giác đồng dạng.
Lời giải chi tiết
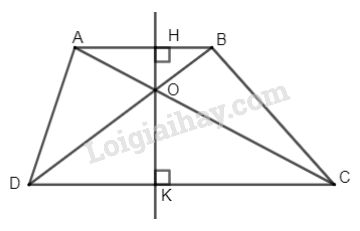
a) Xét hai tam giác \(OAB\) và \(OCD\):
\(\widehat {AOB} = \widehat {COD}\) (hai góc đối đỉnh)
\(\widehat {ABO} = \widehat {ODC}\) (hai góc so le trong vì \(AB//CD\)).
Suy ra \(\Delta OAB \backsim \Delta OCD\) (trường hợp g.g)
Do đó \(\dfrac{{AB}}{{CD}} = \dfrac{{OA}}{{OC}} = \dfrac{{OB}}{{OD}}\) \( \Rightarrow OA.OD = OB.OC\) (đpcm).
b) Xét hai tam giác vuông \(OHB\) và \(OKD\):
\(\widehat {OHB} = \widehat {OKD}\) (cùng bằng \({90^0}\))
\(\widehat {OBH} = \widehat {ODK}\) (hai góc so le trong).
Suy ra \(\Delta OHB \backsim \Delta OKD\)
Do đó \(\dfrac{{OH}}{{OK}} = \dfrac{{OB}}{{OD}}\) (1)
Theo kết quả trên: \(\dfrac{{OB}}{{OD}} = \dfrac{{AB}}{{CD}}\) (2)
Từ (1) và (2) suy ra: \(\dfrac{{OH}}{{OK}} = \dfrac{{AB}}{{CD}}\) (đpcm).
soanvan.me
