Đề bài
Cho tam giác \(ABC\) có các cạnh \(AB = 24 cm,\) \( AC = 28 cm\). Tia phân giác của góc \(A\) cắt cạnh \(BC\) tại \(D\). Gọi \(M, N\) theo thứ tự là hình chiếu của \(B\) và \(C\) trên đường thẳng \(AD\).
a)Tính tỉ số \(\displaystyle {{BM} \over {CN}}\).
b)Chứng minh rằng \(\displaystyle {{AM} \over {AN}} = {{DM} \over {DN}}\) .
Phương pháp giải - Xem chi tiết
a) Xét các cặp tam giác đồng dạng có chứa hai đoạn \(BM,CN\).
Từ đó sử dụng tính chất tam giác đồng dạng suy ra tỉ số cần tìm.
b) Sử dụng kết quả câu a và chứng minh tam giác đồng dạng, từ đó suy ra tỉ số cần chứng minh.
Lời giải chi tiết
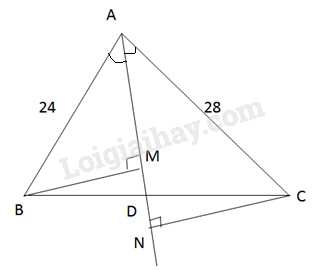
Xét hai tam giác \(ABM\) và \(ACN\).
\(\widehat {BAM} = \widehat {CAN}\) (vì \(AD\) là phân giác của \(\widehat A\))
\(\widehat {BMA} = \widehat {CNA}\) (vì cùng bằng \({90^0}\))
Vậy \(\Delta ABM \backsim \Delta ACN\).
\(\dfrac{{BM}}{{CN}} = \dfrac{{AM}}{{AN}} = \dfrac{{AB}}{{AC}}\) \( \Rightarrow \dfrac{{BM}}{{CN}} = \dfrac{{24}}{{28}} = \dfrac{6}{7}\).
b) Theo chứng minh ở câu a), ta có:
\(\dfrac{{AM}}{{AN}} = \dfrac{{BM}}{{CN}}\) (1)
Xét hai tam giác \(BDM\) và \(CDN\):
\(\widehat {BMD} = \widehat {CND}\) (vì cùng bằng \({90^0}\))
\(\widehat {BDM} = \widehat {CDN}\) (hai góc đối đỉnh)
Vậy: \(\Delta BDM \backsim \Delta CDN\) (trường hợp g.g)
Suy ra \(\dfrac{{BM}}{{CN}} = \dfrac{{DM}}{{DN}}\) (2)
Từ các tỉ lệ thức (1) và (2), suy ra \(\dfrac{{AM}}{{AN}} = \dfrac{{DM}}{{DN}}\) (đpcm).
soanvan.me
