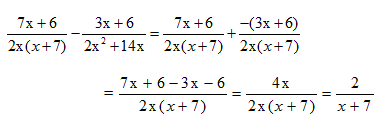Video hướng dẫn giải
Làm các phép tính sau:
LG a
\(\begin{array}{l}
\,\,\dfrac{{4{\rm{x}}y - 5}}{{10{{\rm{x}}^3}y}} - \dfrac{{6{y^2} - 5}}{{10{{\rm{x}}^3}y}}\\
\end{array}\)
Phương pháp giải:
Áp dụng quy tắc trừ hai phân thức:
\(\dfrac{A}{B} - \dfrac{C}{D} = \dfrac{A}{B} + \left( { - \dfrac{C}{D}} \right)\).
Lời giải chi tiết:
\(\begin{array}{l}
\dfrac{{4xy - 5}}{{10{x^3}y}} - \dfrac{{6{y^2} - 5}}{{10{x^3}y}}\\
= \dfrac{{4xy - 5}}{{10{x^3}y}} + \dfrac{{ - \left( {6{y^2} - 5} \right)}}{{10{x^3}y}}\\
= \dfrac{{4xy - 5}}{{10{x^3}y}} + \dfrac{{ - 6{y^2} + 5}}{{10{x^3}y}}\\
= \dfrac{{4xy - 5 - 6{y^2} + 5}}{{10{x^3}y}}\\
= \dfrac{{4xy - 6{y^2}}}{{10{x^3}y}} = \dfrac{{2y\left( {2x - 3y} \right)}}{{2y.5{x^3}}}\\
= \dfrac{{2x - 3y}}{{5{x^3}}}
\end{array}\)
LG b
\(\begin{array}{l}
\,\dfrac{{7{\rm{x}} + 6}}{{2{\rm{x}}\left( {x + 7} \right)}} - \dfrac{{3{\rm{x}} + 6}}{{2{{\rm{x}}^2} + 14{\rm{x}}}}.
\end{array}\)
Phương pháp giải:
Áp dụng quy tắc trừ hai phân thức:
\(\dfrac{A}{B} - \dfrac{C}{D} = \dfrac{A}{B} + \left( { - \dfrac{C}{D}} \right)\).
Lời giải chi tiết:
soanvan.me