Đề bài
Cho \(ABCD\) là tứ giác nội tiếp đường tròn tâm \(M\), biết \(\widehat {DAB} = {80^0},\)\(\widehat {DAM} = {30^0},\)\(\widehat {BMC} = {70^0}\). Hãy tính số đo góc \(MAB;\)\( BCM;\)\( AMB ; DMC ; AMD ; MCD\) và \(BCD\).
Phương pháp giải - Xem chi tiết
+ Sử dụng các định lý: “Trong tứ giác nội tiếp, tổng hai góc đối bằng \(180^\circ \)”; “Tổng ba góc trong tam giác bằng \(180^\circ \)”.
+ Sử dụng tính chất tam giác cân
Lời giải chi tiết
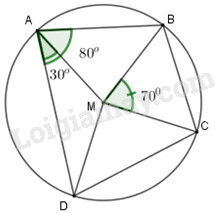
Nối tâm \(M\) của đường tròn với các đỉnh \(A,B,C,D.\)
Vì \(ABCD\) nội tiếp đường tròn ta có :
\(\widehat {DAB} + \widehat {BCD} = 180^\circ \)\( \Leftrightarrow \widehat {BCD} = 180^\circ - 80^\circ = 100^\circ ;\)
\(\widehat {MAB} = \widehat {DAB} - \widehat {DAM}\)\( = 80^\circ - 30^\circ = 50^\circ .\)
+ Xét \(\Delta BMC\) cân vì \(MB = MC\)
Ta có \(\widehat {MBC} = \widehat {BCM}\)
\( \Rightarrow 2\widehat {BCM} = 180^\circ - \widehat {BMC}\)\( = 180^\circ - 70^\circ = 110^\circ .\) Vậy \(\widehat {BCM} = 55^\circ .\)
+ Xét \(\Delta BMA\) cân vì \(MB = MA.\)
Ta có \(\widehat {MAB} = \widehat {ABM}\)\( \Rightarrow \widehat {AMB} = 180^\circ - 2.\widehat {MAB}\)\( = 180^\circ - 2.50^\circ = 80^\circ \) .
Vậy \(\widehat {AMB} = 80^\circ .\)
+ Xét \(\Delta DMA\) cân vì \(MD = MA.\)
Ta có \(\widehat {MAD} = \widehat {ADM}\)\( \Rightarrow \widehat {AMD} = 180^\circ - 2.\widehat {ADM} \)\(= 180^\circ - 60^\circ = 120^\circ .\)
Vậy \(\widehat {AMD} = 120^\circ .\)
Từ các kết quả trên ta có
\(\widehat {DMC} = 360^\circ - \left( {\widehat {AMD} + \widehat {AMB} + \widehat {BMC}} \right) \)\(= 360^\circ - \left( {120^\circ + 80^\circ + 70^\circ } \right) = 90^\circ \)
Vậy \(\widehat {DMC} = 90^\circ \)
Xét \(\Delta DMC\) cân vì \(MD = MC.\) Ta có \(\widehat {MCD} = \widehat {CDM}\)
\( \Rightarrow 2\widehat {MCD} = 180^\circ - \widehat {DMC} \)\(= 180^\circ - 90^\circ = 90^\circ \).
Vậy \(\widehat {MCD} = 45^\circ ,\widehat {BCD} = 100^\circ .\)
soanvan.me
