Đề bài
Cho tam giác đều \(ABC\). Trên nửa mặt phẳng bờ \(BC\) không chứa đỉnh \(A\), lấy điểm \(D\) sao cho \(DB = DC\) và \(\widehat {BCD} = \dfrac{1}{2}\widehat {ACB}.\)
a) Chứng minh \(ABCD\) là tứ giác nội tiếp.
b) Xác định tâm của đường tròn đi qua bốn điểm \(A, B, C, D.\)
Phương pháp giải - Xem chi tiết
Chứng minh tứ giác nội tiếp dựa vào dấu hiệu nhận biết “ tứ giác có tổng hai góc đối bằng là tứ giác nội tiếp”
Lời giải chi tiết
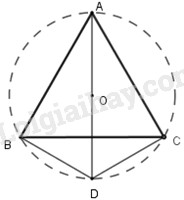

a) Theo giả thiết : \(\widehat {DCB} = \dfrac{1}{2}\widehat {ACB} = 30^\circ \) (1)
\(\widehat {DCB} = \widehat {DBC}\) vì \(\Delta BDC\) cân tại D do \(DB=DC\) (2)
Từ (1) và (2) \( \Rightarrow \widehat {DCB} = \widehat {DBC} = 30^\circ \)
Trong tứ giác \(ABCD\) ta có : \(\widehat {ABD} = \widehat {DBC} + \widehat {CBA} = 30^\circ + 60^\circ\)\( = 90^\circ ;\)
\(\widehat {ACD} = \widehat {DCB} + \widehat {BCA} = 30^\circ + 60^\circ \)\( = 90^\circ \)
nên \(\widehat {ABD} + \widehat {DCA} = 180^\circ .\) Vậy tứ giác \(ABCD\) là tứ giác nội tiếp ( hai góc đối nhau có tổng bằng \(180^\circ \))
b) Vì \(\widehat {ABD} = \widehat {ACD} = 90^\circ \) nên \(AD\) là đường kính đường tròn ngoại tiếp tứ giác \(ABCD.\)
Vậy tâm đường tròn đi qua \(4\) điểm \(A,B,C,D\) là trực tâm của tam giác đều \(ABC\) và là trung điểm của đoạn thẳng \(AD.\)
soanvan.me
