Đề bài
Xem hình 48. Hãy tính số đo các góc của tứ giác ABCD.
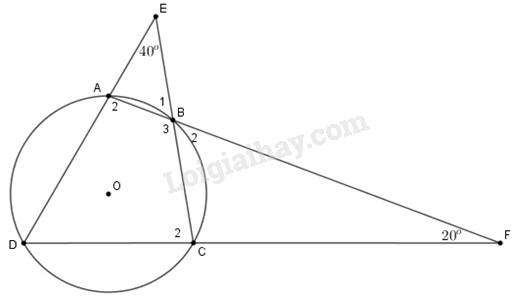
Phương pháp giải - Xem chi tiết
+ Sử dụng các định lý: “Trong tứ giác nội tiếp, tổng hai góc đối bằng \(180^\circ \)”; “Tổng ba góc trong tam giác bằng \(180^\circ \)” và “Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó”
+ Sử dụng tính chất hai góc kề bù
Lời giải chi tiết
Xét \(\Delta ABE\) và \(\Delta CBF,\) ta có \(\widehat {{A_2}} = 40^\circ + \widehat {{B_1}}\,\left( 1 \right)\) vì \(\widehat {{A_2}}\) là góc ngoài tại đỉnh \(E\) của \(\Delta ABE\).
\(\widehat {{C_2}} = \widehat F + \widehat {{B_2}}\,\,\left( 2 \right)\) vì góc ngoài của \(\Delta CBF.\)
Cộng \(\left( 1 \right)\) và \(\left( 2 \right)\) và theo giả thiết ta có : \(\widehat {{A_2}} + \widehat {{C_2}} = 40^\circ + \widehat {{B_1}} + \widehat {{B_2}} + \widehat F\,\,\,\,\,\,\,\,\,\left( 3 \right)\)
Vì \(ABCD\) là tứ giác nội tiếp nên \(\widehat {{A_2}} + \widehat {BCF} = 180^\circ \)và \(\widehat {{B_1}} = \widehat {{B_2}}\) vì hai góc đối đỉnh
Từ \(\left( 3 \right)\) ta có \(180^\circ = 60^\circ + 2\widehat {{B_1}} \Rightarrow \widehat {{B_1}} = 60^\circ .\)
Thay \(\widehat {{B_1}},\widehat {{B_2}}\) vào (1) và (2) ta có : \(\widehat {{A_2}} = 40^\circ + 60^\circ = 100^\circ ;\)
\(\widehat {{C_2}} = 20^\circ + 60^\circ = 80^\circ ;\) \(\widehat {{B_3}} = 180^\circ - \widehat {{B_1}} = 120^\circ \)
Vì \(ABCD\) nội tiếp nên \(\widehat {{B_3}} + \widehat D = 180^\circ \) \( \Rightarrow \widehat D = 180^\circ - \widehat {{B_3}} = 60^\circ \)
Vậy số đo các góc của tứ giác \(ABCD\) là : \(\widehat {{A_2}} = 100^\circ ;\widehat {{C_2}} = 80^\circ ;\widehat {{B_3}} = 120^\circ ;\)\(\widehat D = 60^\circ .\)
soanvan.me
