Đề bài
Cho \({\left( {2x - \frac{1}{3}} \right)^4} = {a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3} + {a_4}{x^4}\). Tính:
a) \({a_2}\)
b) \({a_0} + {a_1} + {a_2} + {a_3} + {a_4}\)
Phương pháp giải - Xem chi tiết
Bước 1: Áp dụng công thức khai triển: \({(a - b)^4} = {a^4} - 4{a^3}b + 6{a^2}{b^2} - 4a{b^3} + {b^4}\) với \(a = 2x,b = \frac{1}{3}\)
Bước 2: Thay x = 1 vào khai triển trong giả thiết để tính tổng các hệ số của khai triển
Lời giải chi tiết
a) Ta có:
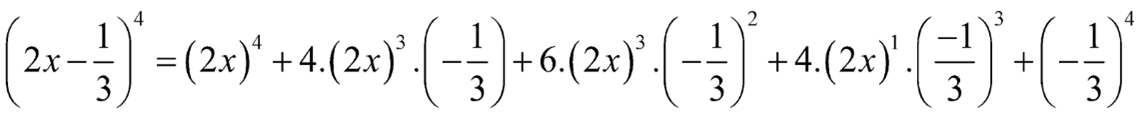
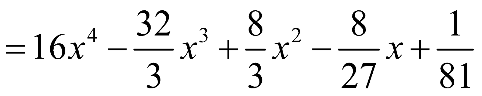
Ta thấy \({a_2}\) là hệ số của \({x^2}\)
Số hạng chứa \({x^2}\) trong khai triển biểu thức \({\left( {2x - \frac{1}{3}} \right)^4}\) là \(\frac{8}{3}{x^2}\)
Suy ra hệ số của trong khai triển biểu thức \({\left( {2x - \frac{1}{3}} \right)^4}\) là \(\frac{8}{3}\)
Vậy \({a_2} = \frac{8}{3}\)
b) Ta có \({\left( {2x - \frac{1}{3}} \right)^4} = {a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3} + {a_4}{x^4}\)
Chọn x = 1, ta được:
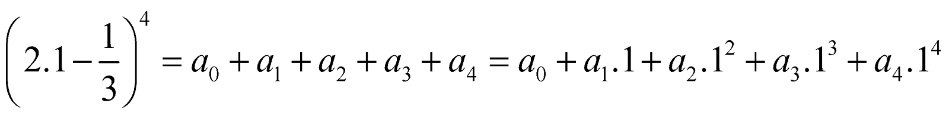
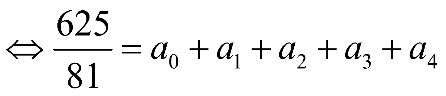
Vậy \({a_0} + {a_1} + {a_2} + {a_3} + {a_4} = \frac{{625}}{{81}}\)
