Đề bài
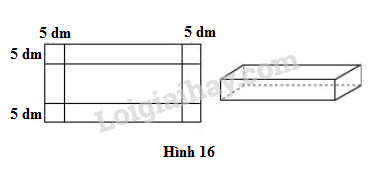
Từ một miếng tôn hình chữ nhật, người ta cắt ở bốn góc bốn hình vuông có cạnh bằng 5 dm để làm thành một cái thùng không nắp có dung tích 1500 dm3 (Hình 16). Hãy tính kích thước của miếng tôn, biết rằng chiều dài của nó gấp đôi chiều rộng.
Phương pháp giải - Xem chi tiết
Sử dụng các bước giải bài toán bằng cách lập phương trình.
Sử dụng công thức tính thể tích (dung tích) hình hộp chữ nhật là \(V = abc\) với \(a\) là chiều dài, \(b\) là chiều rộng và \(c\) là chiều cao của hình hộp chữ nhật.
Lời giải chi tiết
Gọi chiều rộng của miếng tôn là \(x\left( {dm} \right),x > 0.\)
Chiều dài của nó là \(2x\,\left( {dm} \right)\)
Khi làm thành một cái thùng không nắp thì chiều dài của thùng là \(2x - 10\,\left( {dm} \right)\), chiều rộng là \(x - 10\left( {dm} \right)\) ,chiều cao là \(5\left( {dm} \right)\).
Dung tích của thùng là \(\left( {x - 10} \right)\left( {2x - 10} \right).5\,\left( {d{m^3}} \right)\)
Theo đầu bài ta có phương trình \(\left( {x - 10} \right)\left( {2x - 10} \right).5 = 1500\)
Giải phương trình
\(\begin{array}{l}\left( {x - 10} \right)\left( {2x - 10} \right).5 = 1500\\ \Leftrightarrow \left( {x - 10} \right)\left( {2x - 10} \right) = 300\\ \Leftrightarrow 2{x^2} - 30x - 200 = 0\\ \Leftrightarrow {x^2} - 15x - 100 = 0\end{array}\)
Xét \(\Delta = {\left( { - 15} \right)^2} - 4.1.\left( { - 100} \right) = 625 > 0 \)\(\Rightarrow \sqrt \Delta = 25\)
Nên \({x_1} = \dfrac{{15 + 25}}{2} = 20;\) \({x_2} = \dfrac{{15 - 25}}{2} = - 5\)
Vì \(x > 0\) nên \({x_2} = - 5\) bị loại
Trả lời: Miếng tôn có chiều rộng bằng \(20(dm)\) và chiều dài bằng \(2.20 = 40(dm).\)
soanvan.me
