Đề bài
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và SA=2a. Gọi B’, D’ lần lượt là hình chiếu của A trên SB và SD. Mặt phẳng \(\left( {AB'D'} \right)\) cắt SC tại C’. Tính thể tích khối chóp S.AB’C’D’.
Lời giải chi tiết
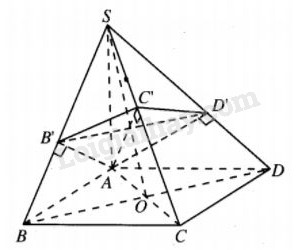
Ta có\(AB' \bot SB,AB' \bot CB(\) do \(CB \bot \left( {SAB} \right)\))
\( \Rightarrow AB' \bot \left( {SBC} \right) \Rightarrow AB' \bot SC \;\;(1)\)
Tương tự \(AD' \bot SC\;\;\;(2)\)
Từ (1) và (2) suy ra
\(\eqalign{ & SC \bot \left( {AB'C'D'} \right) \cr & \Rightarrow SC \bot AC'. \cr} \)
Do tính đối xứng ta có
\({V_{S.AB'C'D'}} = 2{V_{S.AB'C'}}\)
Ta có
\(\eqalign{ & {{{V_{S.AB'C'}}} \over {{V_{S.ABC}}}} = {{SB'} \over {SB}}.{{SC'} \over {SC}} = {{SB'.SB} \over {S{B^2}}}.{{SC'.SC} \over {S{C^2}}} \cr & = {{S{A^2}} \over {S{B^2}}}.{{S{A^2}} \over {S{C^2}}} = {{4{a^2}} \over {5{a^2}}}.{{4{a^2}} \over {6{a^2}}} = {8 \over {15}}. \cr & {V_{S.ABC}} = {1 \over 3}.{{{a^2}} \over 2}.2a = {{{a^3}} \over 3}\cr& \Rightarrow {V_{S.AB'C'}} = {8 \over {15}}.{{{a^3}} \over 3} = {{8{a^3}} \over {45}} \cr & \Rightarrow {V_{S.AB'C'D'}} = {{16{a^3}} \over {45}}. \cr} \)
soanvan.me
