Cho khối lập phương ABCD.A’B’C’D’ cạnh a. Các điểm E và F lần lượt là trung điểm của C’B’ và C’D’.
LG a
Dựng thiết diện của khối lập phương khi cắt bởi \(mp\left( {AEF} \right).\)
Lời giải chi tiết:
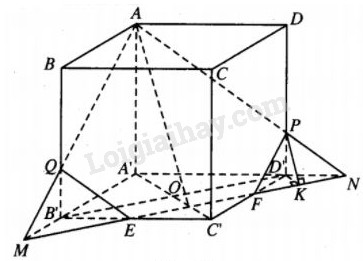
Đường thẳng EF cắt A’D’ tại N, cắt A’B’ tại M, AN cắt DD’ tại P, AM cắt BB’ tại Q.
Vậy thiết diện là ngũ giác APFEQ.
LG b
Tính tỉ số thể tích hai phần của khối lập phương bị chia bởi mặt phẳng \(\left( {AEF} \right).\)
Lời giải chi tiết:
Đặt :
\(\eqalign{ & V = {V_{ABCD.A'B'C'D'}}, \cr & {V_1} = {V_{ABCDC'QEFP}}, \cr & {V_2} = {V_{AQEFP.B'A'D'}}, \cr & {V_3} = {V_{A.MA'N}}, \cr & {V_4} = {V_{PFD'N}},{V_5} = {V_{QMB'E}}. \cr} \)
Dễ thấy \({V_4} = {V_5}\) ( do tính đối xứng của hình lập phương),
\(\eqalign{ & {V_3} = {1 \over 6}AA'.A'M.A'N = {1 \over 6}a.{{3a} \over 2}.{{3a} \over 2} = {{3{a^3}} \over 8}, \cr & {V_4} = {1 \over 6}PD'.D'F.D'N = {1 \over 6}.{a \over 3}.{a \over 2} .{a \over 2} = {{{a^3}} \over {72}}, \cr & {V_2} = {V_3} - 2{V_4} = {{3{a^3}} \over 8} - {{2{a^3}} \over {72}} = {{25{a^3}} \over {72}}, \cr & {V_1} = V - {V_2} = {a^3} - {{25{a^3}} \over {72}} = {{47} \over {72}}{a^3}. \cr} \)
Mặt phẳng \(\left( {AEF} \right)\) chia khối lập phương thành hai phần lần lượt có thể tích là \({V_1} = {{47} \over {72}}{a^3},{V_2} = {{25{a^3}} \over {72}}.\)
Vậy : \({{{V_1}} \over {{V_2}}} = {{47} \over {25}}.\)
soanvan.me
