Đề bài
Bốn đường thẳng \({\Delta _1},{\Delta _2},{\Delta _3},{\Delta _4}\) đôi một song song và không có ba đường thẳng nào trên cùng một mặt phẳng. Một mặt phẳng \(\left( P \right)\) cắt chúng theo thứ tự tại A, B, C, D. Một mặt phẳng \(\left( {P'} \right)\) cắt chúng theo thứ tự A’, B’, C’, D’. Chứng minh hai khối tứ diện D’ABC và DA’B’C’ có thể tích bằng nhau.
Lời giải chi tiết
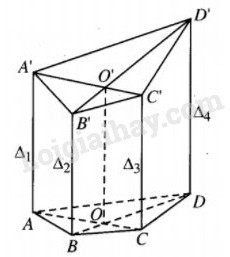
Gọi \(O = AC \cap BD,O' = A'C' \cap B'D'.\)
Do \(DD'//OO'\) nên dễ thấy
\({{d\left( {D',\left( {ABC} \right)} \right)} \over {d\left( {O',\left( {ABC} \right)} \right)}} = {{DD'} \over {OO'}},{{d\left( {D,\left( {A'B'C'} \right)} \right)} \over {d\left( {O,\left( {A'B'C'} \right)} \right)}} = {{DD'} \over {OO'}}.\)
Vậy :
\(\left. \matrix{ {V_{D'.ABC}} = {{DD'} \over {OO'}}{V_{O'.ABC}} \hfill \cr {V_{D.A'B'C'}} = {{DD'} \over {OO'}}{V_{O.A'B'C'}} \hfill \cr} \right\}\;\;\;\;\;(1)\)
Đặt \(h = d\left( {BB',\left( {ACC'A'} \right)} \right).\)
Ta có \(h = d\left( {B,\left( {ACC'A'} \right)} \right)\) và
\(\eqalign{ & {V_{O'.ABC}} = {V_{B.O'AC}} = {1 \over 3}h.{S_{O'AC}}\;\;\;\;\;(2) \cr & {V_{O.A'B'C'}} = {V_{B'.OA'C'}} = {1 \over 3}h.{S_{OA'C'}}\;\;\;(3) \cr} \)
Đặt \(d = d\left( {AA',CC'} \right)\) thì \(\eqalign{ & {S_{O'AC}} = {S_{OA'C'}} = {1 \over 2}OO'.d\;\;\;\;(4) \cr & {S_{O'AC}} = {S_{AOO'}} + {S_{COO'}} \cr&\;\;\;\;\;\;\;\;\;\;= {1 \over 2}OO'\left( {d\left( {A,OO'} \right) + d\left( {C.OO'} \right)} \right) \cr&\;\;\;\;\;\;\;\;\;\;= {1 \over 2}OO'.d \cr} \)
Tương tự \({S_{OA'C'}} = {1 \over 2}OO'.d\).
Từ (2), (3), (4) suy ra \({V_{O'.ABC}} = {V_{O.A'B'C'}}\;\;\;\;(5)\)
Từ (1) và (5) ta suy ra \({V_{D'.ABC}} = {V_{D.A'B'C'}}.\)
soanvan.me
