Video hướng dẫn giải
Các câu sau đúng hay sai ?
LG a.
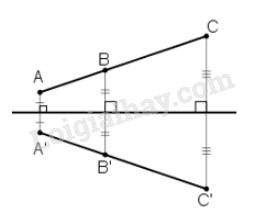
Nếu ba điểm thẳng hàng thì ba điểm đối xứng với chúng qua một trục cũng thẳng hàng.
Phương pháp giải:
- Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \( d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
- Hai hình gọi là đối xứng với nhau qua đường thẳng \(d\) nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng \(d\) và ngược lại.
- Đường thẳng \(d\) gọi là trục đối xứng của hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua đường thẳng \(d\) cũng thuộc hình \(H.\)
Lời giải chi tiết:
Đúng.
LG b.
Hai tam giác đối xứng với nhau qua một trục thì có chu vi bằng nhau.
Phương pháp giải:
- Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \( d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
- Hai hình gọi là đối xứng với nhau qua đường thẳng \(d\) nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng \(d\) và ngược lại.
- Đường thẳng \(d\) gọi là trục đối xứng của hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua đường thẳng \(d\) cũng thuộc hình \(H.\)
Lời giải chi tiết:
Đúng vì hai tam giác đối xứng nhau qua một trục thì bằng nhau nên chúng cũng có chu vi bằng nhau.
LG c.
Một đường tròn có vô số trục đối xứng.
Phương pháp giải:
- Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \( d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
- Hai hình gọi là đối xứng với nhau qua đường thẳng \(d\) nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng \(d\) và ngược lại.
- Đường thẳng \(d\) gọi là trục đối xứng của hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua đường thẳng \(d\) cũng thuộc hình \(H.\)
Lời giải chi tiết:
Đúng vì tất cả các đường thẳng đi qua tâm đều là trục đối xứng của đường tròn.
LG d.
Một đoạn thẳng chỉ có một trục đối xứng.
Phương pháp giải:
- Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \( d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
- Hai hình gọi là đối xứng với nhau qua đường thẳng \(d\) nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng \(d\) và ngược lại.
- Đường thẳng \(d\) gọi là trục đối xứng của hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua đường thẳng \(d\) cũng thuộc hình \(H.\)
Lời giải chi tiết:
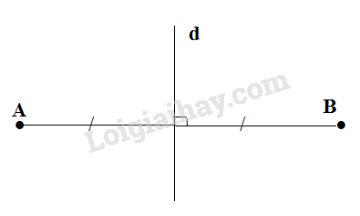
Sai.
Giải thích: Đoạn thẳng \(AB\) trên hình bên có hai trục đối xứng đó là đường thẳng \(AB\) và đường trung trực của đoạn \(AB.\)
soanvan.me
