Đề bài
Cho tam giác ABC cân tại A. Lấy M bất kì thuộc cạnh BC, kẻ \(MD \bot AB,ME \bot AC.\) Gọi \(D'\) là điểm đối xứng của D qua BC.
a) Chứng minh ba điểm E, M, \(D'\) thẳng hàng.
b) Kẻ \(BF \bot AC.\) Chứng minh \(ED' = BF.\)
Phương pháp giải - Xem chi tiết
+) Sử dụng định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng dd nếu dd là đường trung trực của đoạn thẳng nối hai điểm đó.
+) Sử dụng tính chất đường trung trực: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
+) Trong tam giác cân, đường trung tuyến ứng với cạnh đáy cũng là đường trung trực, đường phân giác.
Lời giải chi tiết
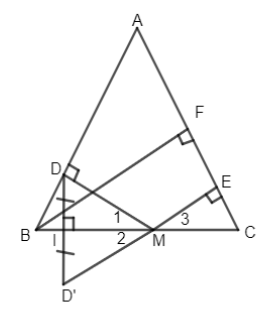
a) D' đối xứng với D qua BC \( \Rightarrow DD' \bot BC\) và \(ID' = ID\) (I là giao điểm của \(DD'\) và \(BC\)
Suy ra tam giác MDD' có MI vừa là đường trung tuyến vừa là đường cao
\( \Rightarrow \Delta DMD'\) cân tại M, do đó đường cao MI đồng thời là phân giác: \(\widehat {{M_1}} = \widehat {{M_2}}\) , mà \(\widehat {{M_1}} = \widehat {{M_3}}\) (cùng phụ với \(\widehat B = \widehat C\) ) \( \Rightarrow \widehat {{M_2}} = \widehat {{M_3}}\) mà \(\widehat {{M_3}} + \widehat {EMB} = {180^ \circ }\)
\( \Rightarrow \widehat {{M_2}} + \widehat {EMB} = {180^ \circ }\) chứng tỏ \(E,M,D'\) thẳng hàng.
b) Vì tam giác MDD' cân tại M nên \(MD=MD'\)
Xét \(\Delta BDM\) và \(\Delta BD’M\) có:
\(MD=MD'\) (cmt)
\(\widehat {{M_1}} = \widehat {{M_2}}\) (cmt)
Cạnh MB chung
Suy ra \(\Delta BDM = \Delta BD’M\left( {c.g.c} \right)\)
\( \Rightarrow \widehat {BD’M} = \widehat {BDM} = {90^ \circ }\) hay \(D’B \bot D’E \Rightarrow D’B//EF.\)
Lại có \(BF// D’E\left( { \bot AC} \right)\) nên \(BFED’\) là hình thang có hai cạnh bên song song \( \Rightarrow ED’= BF.\)
soanvan.me
