Đề bài
Cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) khác vectơ \(\overrightarrow 0 \). Chứng minh rằng nếu hai vectơ cùng hướng thì \(\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = \left| {\overrightarrow a + \overrightarrow b } \right|\)
Phương pháp giải - Xem chi tiết
Bước 1: Dựng 2 vectơ \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \) thỏa mãn \(\overrightarrow {AB} ,\overrightarrow {BC} \)cùng hướng
Bước 2: Sử dụng quy tắc cộng vectơ và độ dài vectơ để biến đổi giả thiết \(\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = \left| {\overrightarrow a + \overrightarrow b } \right|\)
Lời giải chi tiết
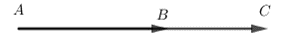
Lấy một điểm A trên mặt phẳng. Dựng \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \) sao cho \(\overrightarrow {AB} ,\overrightarrow {BC} \)cùng hướng
\( \Rightarrow \left| {\overrightarrow a } \right| = AB,\left| {\overrightarrow b } \right| = BC\)
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \Leftrightarrow \overrightarrow a + \overrightarrow b = \overrightarrow {AC} \)
Lại có: AB + BC = AC \( \Rightarrow \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = AC = \left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow a + \overrightarrow b } \right|\) (ĐPCM)
