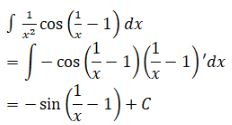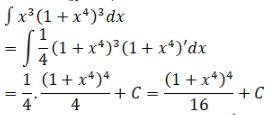LG a
\(y = {1 \over {{x^2}}}\cos \left( {{1 \over x} - 1} \right)\);
Phương pháp giải:
Đổi biến \(u = {1 \over x} - 1\)
Lời giải chi tiết:
Đặt \(u = {1 \over x} - 1 \Rightarrow du = - {1 \over {{x^2}}}dx \) \(\Rightarrow {{dx} \over {{x^2}}} = - du\)
Do đó \(\int {{1 \over {{x^2}}}} \cos \left( {{1 \over x} - 1} \right)dx = - \int {\cos udu}\) \( = - \sin u + C = - \sin \left( {{1 \over x} - 1} \right) + C\)
Cách 2: Đưa vào vi phân
LG b
\(y = {x^3}{\left( {1 + {x^4}} \right)^3}\);
Phương pháp giải:
Đổi biến \(u=1+x^4\)
Lời giải chi tiết:
Đặt \(u = 1 + {x^4} \Rightarrow du = 4{x^3}dx \) \(\Rightarrow {x^3}dx = {{du} \over 4}\)
\(\int {{x^3}{{\left( {1 + {x^4}} \right)}^3}dx}= {1 \over 4}\int {{u^3}du} \) \(= {{{u^4}} \over {16}} + C \) \(= {1 \over {16}} {\left( {1 + {x^4}} \right)^4} + C\)
Cách 2: Đưa vào vi phân
LG c
\(y = {{x{e^{2x}}} \over 3}\);
Phương pháp giải:
Sử dụng phương pháp từng phần tính nguyên hàm:
Đặt \(\left\{ \matrix{u = {x \over 3} \hfill \cr dv = {e^{2x}}dx \hfill \cr} \right. \)
Lời giải chi tiết:
Đặt
\(\left\{ \matrix{
u = {x \over 3} \hfill \cr
dv = {e^{2x}}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = {1 \over 3}dx \hfill \cr
v = {1 \over 2}{e^{2x}} \hfill \cr} \right.\)
Suy ra: \(\int {{{x{e^{2x}}} \over 3}}dx \) \(= {1 \over 6}x{e^{2x}} - {1 \over 6}\int {{e^{2x}}dx} \) \(= {1 \over 6}x{e^{2x}} - {1 \over {12}}{e^{2x}} + C \)
LG d
\(y = {x^2}{e^x}\).
Phương pháp giải:
Đặt
\(\left\{ \matrix{
u = {x^2} \hfill \cr
dv = {e^x}dx \hfill \cr} \right. \)
Lời giải chi tiết:
Đặt
\(\left\{ \matrix{
u = {x^2} \hfill \cr
dv = {e^x}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = 2xdx \hfill \cr
v = {e^x} \hfill \cr} \right.\)
Suy ra \(\int {{x^2}{e^x}dx = {x^2}{e^x} - 2\int {x{e^x}dx} } \) (1)
Đặt
\(\left\{ \matrix{
u = x \hfill \cr
dv = {e^x}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = {e^x} \hfill \cr} \right.\)
Do đó: \(\int {x{e^x}dx }\) \(= x{e^x} - \int {{e^x}dx}\) \( = x{e^x} - {e^x} + C_1 \)
Từ (1) suy ra \(\int {{x^2}{e^x}dx} = {x^2}{e^x} - 2x{e^x} + 2{e^x} + C \) \(= {e^x}\left( {{x^2} - 2x + 2} \right) + C\)
soanvan.me