Đề bài
Hai đường chéo của một hình thoi có độ dài là \(16\,cm\) và \(12\,cm.\) Tính:
a) Diện tích hình thoi
b) Độ dài cạnh hình thoi
c) Độ dài đường cao hình thoi
Phương pháp giải - Xem chi tiết
Diện tích hình thoi bằng một nửa tích độ dài hai đường chéo: \(S =\dfrac{1}{2} {d_1}.{d_2}\)
Diện tích hình thoi bằng tích của cạnh đáy với chiều cao: \(S=a.h\)
Lời giải chi tiết
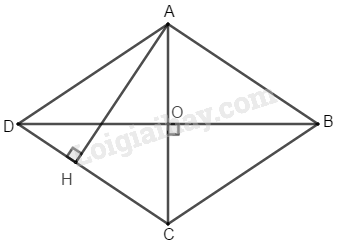
Giả sử ABCD là hình thoi có \(AC=12cm, BD=16cm\) và O là giao điểm hai đường chéo
Suy ra \(AC \bot BD\) và \(O\) là trung điểm của AC, BD.
Do đó \(OA = \dfrac{{AC}}{2};OB = \dfrac{{BD}}{2}\)
a. \(S_{ABCD} = AC.BD = \dfrac{1}{2}.12.16 = 96\) \((cm^2)\)
b.Trong tam giác vuông \(OAB\), theo định lý Pytago ta có:
\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} \\= {\left( {\dfrac{{AC}}{2}} \right)^2} + {\left( {\dfrac{{BD}}{2}} \right)^2} \\= {6^2} + {8^2} = 100\\ \Rightarrow AB = 10(cm)\end{array}\)
Vậy cạnh hình thoi là \(10cm\).
c. Kẻ \(AH ⊥ CD\) (\(H ∈ CD\))
\(\eqalign{ & {S_{ABCD}} = AH.CD \cr & \Rightarrow AH = {{{S_{ABCD}}} \over {CD}} = {{96} \over {10}} = 9,6(cm) \cr} \)
soanvan.me
