Đề bài
Cho tam giác đều ABC có cạnh bằng a. Tính độ dài của các vectơ \(\overrightarrow {AB} - \overrightarrow {AC} ,\;\overrightarrow {AB} + \overrightarrow {AC} .\)
Phương pháp giải - Xem chi tiết
Với 3 điểm A, B, C bất kì, ta có: \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \)
Tứ giác MNPQ là hình bình hành thì \(\overrightarrow {MN} + \overrightarrow {MQ} = \overrightarrow {MP} \)
Lời giải chi tiết
\(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = CB = a.\)
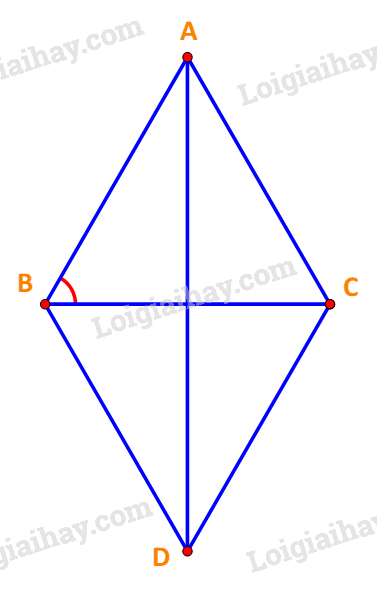
Dựng hình bình hành ABDC tâm O như hình vẽ.
Ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
\( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Vì tứ giác ABDC là hình bình hành, lại có \(AB = AC = BD = CD = a\) nên ABDC là hình thoi.
\( \Rightarrow AD = 2AO = 2.AB.\sin B = 2a.\frac{{\sqrt 3 }}{2} = a\sqrt 3 .\)
Vậy \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = a\) và \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \).
