Đề bài
Cho tam giác ABC cân tại A. Trên cạnh BC lần lượt lấy hai điểm M và N sao cho MN = MN = NC. Gọi H là trung điểm của BC.
a) Chứng minh rằng AM = AN.
b) Chứng minh rằng \(AH \bot BC.\)
c) Cho biết AB = 5 cm, BC = 6 cm. Tính AM.
Lời giải chi tiết
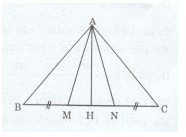
a)Xét tam giác ABM và CAN ta có:
AB = AC (tam giác ABC cân tại A)
\(\widehat {ABM} = \widehat {ACN}(\Delta ABC\) cân tại A)
BM = CN (giả thiết)
Do đó: \(\Delta ABM = \Delta ACN(c.g.c) \Rightarrow AM = AN.\)
b)Xét hai tam giác ABH và ACH ta có:
AB = AC (tam giác ABC cân tại A)
BH = CH (H là trung điểm BC)
AH là cạnh chung.
Do đó: \(\Delta ABH = \Delta ACH(c.c.c) \Rightarrow \widehat {AHB} = \widehat {AHC}.\)
Mà \(\widehat {AHB} + \widehat {AHC} = {180^0}\) (hai góc kề bù)
Nên \(\widehat {AHB} + \widehat {AHB} = {180^0} \Rightarrow 2\widehat {AHB} = {180^0} \Rightarrow \widehat {AHB} = {90^0}.\) Vậy \(AH \bot BC.\)
c) Ta có: \(\eqalign{ & BH = HC = {{BC} \over 2} = {6 \over 2} = 3cm \cr & BM = MN = NC = {{BC} \over 2} = {6 \over 3} = 2cm \cr & BM + MH = BH \Rightarrow MH = BH - BM = 3 - 2 = 1(cm). \cr} \)
Tam giác ABH vuông tại H \(\Rightarrow A{B^2} = A{H^2} + B{H^2}\) (định lí Pythagore)
Do đó: \(A{H^2} = A{B^2} - B{H^2} = {5^2} - {3^2} = 16,AH > 0\) Vậy \(AH = \sqrt {16} = 4(cm).\)
Tam giác AMH vuông tại H \(\Rightarrow A{M^2} = A{H^2} + M{H^2}\) (định lí Pythagore)
Do đó: \(A{M^2} = {4^2} + {1^2} = 16 + 1 = 17\)
Mà AM > 0. Vậy \(AM = \sqrt {17} (cm).\)
soanvan.me
