Đề bài
Cho tam giác ABC vuông tại A. GỌi M là trung điểm của BC, trên tia đối của tia MA lấy điểm D sao cho M là trung điểm của AD.
a) Chứng minh rằng \(\Delta MAB = \Delta MDC.\)
b) Chứng minh rằng \(CD \bot AC.\)
c) Gọi N là trung điểm của AC. Chứng minh rằng NB = ND.
d) Cho \(\widehat {ABC} = {60^0}.\) Chứng minh rằng \(\Delta MAB\) đều. Tinh AC khi biết AB = 8 cm.
Lời giải chi tiết
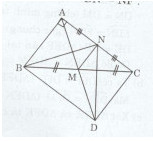
a)Xét tam giác MAB và MDC có:
MA = MD (M là trung điểm của AD)
MB = MC (M là trung điểm của BC)
\(\widehat {AMB} = \widehat {DMC}\) (hai góc đối đỉnh)
Do đó: \(\Delta MAB = \Delta MDC(c.g.c).\)
b) Ta có: \(\widehat {ABM} = \widehat {DCM}(\Delta MAB = \Delta MDC)\)
Mà góc ABM và DCM so le trong. Do đó: AB // CD.
Ta có: \(AB \bot AC(\Delta ABC\) vuông tại A) và AB // CD (chứng minh trên) \(\Rightarrow CD \bot AC.\)
c) Xét tam giác ANB và CND ta có:
AN = CN (N là trung điểm của AC)
\(\eqalign{ & \widehat {BAN} = \widehat {NCD}( = {90^0}) \cr & AB = CD(\Delta MAB = \Delta MDC) \cr} \)
Do đó: \(\Delta ANB = \Delta CND(c.g.c) \Rightarrow NB = ND\)
d) Xét tam giác ABC và CDA có:
AB = CD
\(\widehat {BAC} = \widehat {DCA}( = {90^0})\)
AC là cạnh chung.
Do đó: \(\Delta ABC = \Delta CDA(c.g.c) \Rightarrow BC = AD\)
Mà \(MB = MC = {{BC} \over 2}\) (M là trung điểm của BC)
Và \(MA = MD = {{AD} \over 2}\) (M là trung điểm của AD)
Do đó: MB = MC = MA = MD.
Tam giác MAB có MB = MA => tam giác MAB cân tại M
Mà \(\widehat {ABC} = {60^0}(gt)\) . Do đó tam giác MAB đều => MB = AB = 8cm.
Ta có: BC = 2MB = 2.8 = 16 (cm)
Tam giác ABC vuông tại A
\(\Rightarrow A{B^2} + A{C^2} = B{C^2}\) (định lí Pythagore)
Do đó: \(A{C^2} = B{C^2} - A{B^2} = {16^2} - {8^2} = 256 - 64 = 192\)
Mà AC > 0. Vậy \(AC = \sqrt {192} (cm).\)
soanvan.me
