Đề bài
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H. Tia phân giác của góc HAC cắt BC tại D. Lấy \(K \in AB\) sao cho BK = BH. Chứng minh rằng : KH // AD.
Lời giải chi tiết
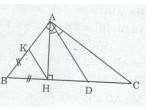
Ta có: BK = BH (giả thiết) => tam giác BHK cân tại B \(\Rightarrow \widehat {BKH} = \widehat {BHK}\)
Mà \(\widehat {KBH} + \widehat {BHK} + \widehat {BKH} = {180^0}\) (tổng ba góc trong một tam giác)
Nên \(\eqalign{ & \widehat {BHK} + \widehat {BHK} + \widehat {KBH} = {180^0} \cr & \Rightarrow 2\widehat {BHK} + \widehat {KBH} = {180^0} \Rightarrow \widehat {BHK} = {{{{180}^0} - \widehat {KBH}} \over 2}(1) \cr} \)
Mặt khác \(\widehat {BAD} + \widehat {DAC} = \widehat {BAC} = {90^0} \Rightarrow \widehat {BAD} = {90^0} - \widehat {DAC}.\)
Và \(\widehat {BDA} + \widehat {HAD} = {90^0}(\Delta HAD\) vuông tại H) \(\Rightarrow \widehat {BAD} = {90^0} - \widehat {HAD}\)
Mà \(\widehat {DAC} = \widehat {HAD}\) (AD là tia phân giác của góc HAC). Do đó: \(\widehat {BAD} = \widehat {BDA}\)
Tam giác ABD có: \(\widehat {KBH} + \widehat {BAD} + \widehat {BDA} = {180^0}.\)
Do đó: \(\widehat {BDA} = {{{{180}^0} - \widehat {KBH}} \over 2}(2)\)
Từ (1) và (2) ta có: \(\widehat {BHK} = \widehat {BDA}\)
Mà góc BHK và BDA đồng vị. Vậy KH // AD.
soanvan.me
