Bài 5 trang 200 SBT hình học 11

Đề bài

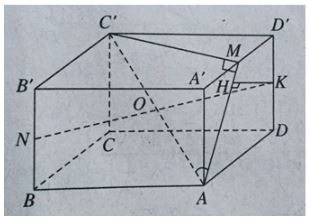
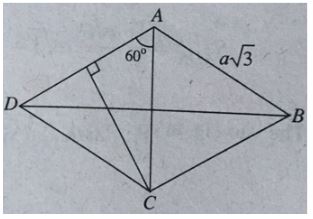
Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, AB = a√3, ∠BAD = 120^o. Góc giữa đường thẳng AC' và mặt phẳng (ADD'A') là 30 ^o. Gọi M là trung điểm A'D', N là trung điểm BB'. Tính khoảng cách từ N đến mặt phẳng (C'MA)

Lời giải chi tiết

Nhận xét:

Do tam giác A’B’D’ là tam giác đều nên C’M ⊥ A’D’

(C'A'D') ⊥ (AA'D'D) & (C'A'D') ∩(AA'D'D) ⇒ C’M ⊥ (AA’D’D)

Nên ∠(AC',(AA'D'D)) = ∠(C'AM) = 30^o.

Gọi K là trung điểm của DD’, ta có AKC’N là hình bình hành nên K với N đối xứng nhau qua trung điểm O của AC’. Mà O ∈ (AMC’), do đó

d(N,(C'MA)) = d(K,(C'MA))

+ Xác định khoảng cách từ K đến (C’MA).

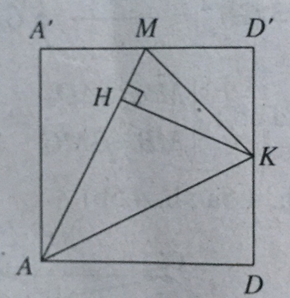
Do (C’MA) vuông góc với (AA’D’D) theo giao tuyến AM nên kẻ KH ⊥ AM, ta có KH ⊥ (C’MA) hay d[K,(C'MA)] = KH.

+ Tính KH.

Ta có: S_AMK = S_AA'D'D – (S_AA'M + S_MD'K + S_ADK) (1)

Trong tam giác AMC’, ta có: AM = C’M.cot30^o = (3a√3)/2.

Trong tam giác AA’M, ta có: AA’ = √(AM² - A'M² ) = a√6.

soanvan.me