Đề bài
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a. Gọi E là điểm đối xứng của D qua trung điểm SA, M là trung điểm của AE, N là trung điểm của BC. Chứng minh rẳng MN vuông góc với BD và tính khoảng cách giữa hai đường thẳng MN và AC.
Lời giải chi tiết
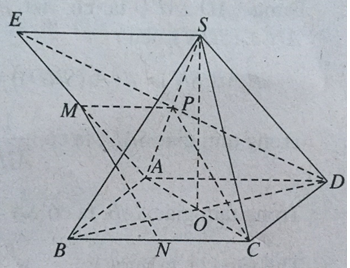
Gọi P là trung điểm SA, ta có MPCN là hình bình hành.
Như vậy MN // PC, suy ra MN // (SAC).
Do BD ⊥ (SAC) nên BD ⊥ MN.
Ta có: d(MN, AC) = d(N, (SAC))
Mà C ∈(SAC) & CN/CB = 1/2
Nên d(N, (SAC)) = 1/2 d(B, (SAC)) = 1/2 BO (O là giao điểm của AC và BD).
Vậy d(N, (SAC)) = 1/4a√2.
soanvan.me
