Đề bài
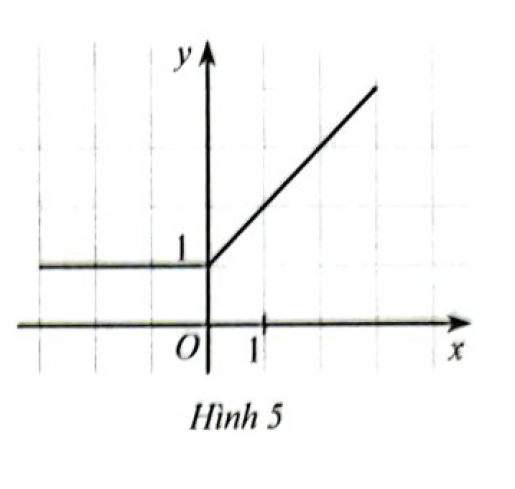
Quan sát đồ thị hàm số \(y = f\left( x \right)\) ở Hình 5
a) Trong các điểm có tọa độ (1;2), (0;0). (2;3) điểm nào thuộc đồ thị hàm số, điểm nào không thuộc đồ thị hàm số?
b) Xác định \(f\left( 0 \right),f\left( 3 \right)\)
c) Tìm điểm thuộc đồ thị hàm số có tung độ bằng 1
Phương pháp giải - Xem chi tiết
Với\(f\left( x \right) = a{x^2} + bx + c \Rightarrow x = {x_0};f\left( {{x_0}} \right) = a{x_0}^2 + b{x_0} + c\)
Lời giải chi tiết
a)
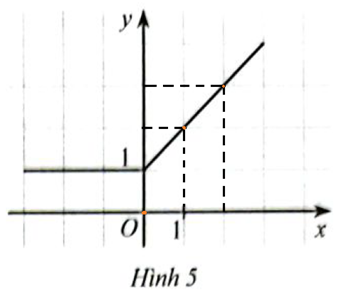
Quan sát đồ thị, ta thấy điểm có tọa độ (0;0) không thuộc đồ thị hàm số. Các điểm có tọa độ (1;2), (2;3) thuộc đồ thị hàm số.
b) + Tại \(x = 0,f\left( 0 \right) = 1\)
+ Tại \(x = 3,f\left( 3 \right) = 4\)
c) Ta thấy: các điểm thuộc đồ thị, nằm bên trái trục tung đều có tung độ bằng 1.
Do đó các điểm thuộc đồ thị tung độ bằng 1 là \(A = \{ (a;0)|a \in \mathbb{R},a \le 0\} \)
