Đề bài
Cho tam giác đều \(ABC\). Gọi \(O\) là tâm của đường tròn đi qua ba đỉnh \(A, B, C\)
a) Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính \(OA, OB, OC\)
b) Tính số đo các cung tạo bởi hai trong ba điểm \(A, B, C\)
Phương pháp giải - Xem chi tiết
Sử dụng tính chất tam giác đều và tính chất hai tam giác bằng nhau
Sử dụng cả đường tròn có số đo bằng \(360^\circ .\)
Lời giải chi tiết
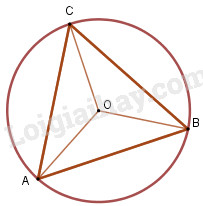

a) Từ giả thiết ta có \(\Delta AOC = \Delta AOB = \Delta COB\) (c - c - c)
suy ra \(\widehat {AOC} = \widehat {BOC} = \widehat {AOB}\) (các góc tương ứng)
mà \(\widehat {ACB}=60^0\)\( \Rightarrow \widehat {AOB} = \widehat {AOC} = \widehat {BOC} \)\( = 120^\circ \)
b) Từ câu a) suy ra \(sđ\overparen{AC}=sđ\overparen{BC}=sđ\overparen{AB}\)\( = 120^\circ \)
Suy ra sđ\(\overparen{ABC}\) = sđ\(\overparen{BAC}\) = sđ\(\overparen{ACB}\) \( = 360^\circ - 120^\circ = 240^\circ \)
soanvan.me
