Đề bài
Trên đường tròn tâm \(O\) lấy ba điểm \(A, B, C\) sao cho \(\widehat {AOB} = {100^o}\) . Số đo cung \(AC\) bằng \(45\)o. Tính số đo cung nhỏ \(BC\) và cung lớn \(BC\) (xét cả hai trường hợp: điểm \(C\) nằm trên cung nhỏ \(AB\), điểm \(C\) nằm trên cung lớn \(AB\)).
Phương pháp giải - Xem chi tiết
Sử dụng: Nếu \(C\) là một điểm nằm trên cung \(AB\) thì số đo cung \(AB = \)số đo cung \(AC + \) số đo cung \(BC\).
Lời giải chi tiết
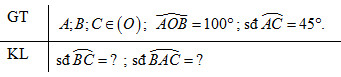
a) Điểm \(C\) nằm trên cung nhỏ \(AB.\)

sđ\(\overparen{BC}=\) sđ\(\overparen{AB}-\) sđ\(\overparen{AC}\)\( = 100^\circ - 45^\circ = 55^\circ \)
sđ\(\overparen{BAC}= 360^\circ - 55^\circ = 305^\circ \)
b) Điểm \(C\) nằm trên cung lớn \(AB.\)

sđ\(\overparen{BAC}=\) sđ\(\overparen{AC}+\) sđ\(\overparen{AB}\)\( = 100^\circ + 45^\circ = 145^\circ \)
sđ\(\overparen{BC}= 360^\circ - 145^\circ = 215^\circ \)
soanvan.me
