Đề bài
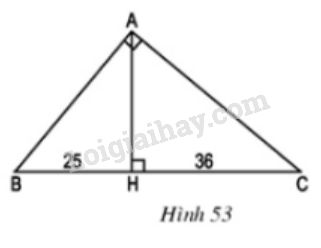
Chân đường cao \(AH\) của tam giác vuông \(ABC\) chia cạnh huyền \(BC\) thành hai đoạn có độ dài \(25cm\) và \(36cm\). Tính chu vi và diện tích của tam giác vuông đó (h.53)
Hướng dẫn: Trước tiên tìm cách \(AH\) từ các tam giác vuông đồng dạng, sau đó tính các cạnh của tam giác \(ABC.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng tính chất hai tam giác đồng dạng, định lí py-ta-go, công thức tính chu vi, diện tích tam giác.
Lời giải chi tiết
\(∆AHB ∽ ∆CHA\) (g.g) vì \(\widehat{AHB} = \widehat{AHC}=90^o\) , \(\widehat{BAH} = \widehat{ACH}\) (cùng phụ với \(\widehat {HAC}\))
\( \Rightarrow \dfrac{AH}{CH }= \dfrac{BH}{AH}\)
\( \Rightarrow A{H^2}=CH.BH = 25.36\)
\( \Rightarrow A{H^2}= 900 \Rightarrow AH = 30cm\)
Vậy \(S_{ABC} = \dfrac{1}{2}.AH.BC \)\(\,= \dfrac{1}{2}.30.(25 + 36) = 915 \) cm2
Áp dụng Py-ta-go cho 2 tam giác vuông \(ABH\) và \(ACH\) ta được:
\(\begin{array}{l}
A{B^2} = B{H^2} + A{H^2}\\
\Rightarrow A{B^2} = {25^2} + {30^2} = 1525\\ \Rightarrow AB \approx 39,05cm\\
A{C^2} = C{H^2} + A{H^2}\\
\Rightarrow A{C^2} = {36^2} + {30^2} = 2196\\ \Rightarrow AC \approx 46,86cm
\end{array}\)
Chu vi tam giác ABC là: \(P = AB + AC + BC \) \(= 39,05 + 46,86 + 61 = 146,91cm\)
soanvan.me
