Đề bài
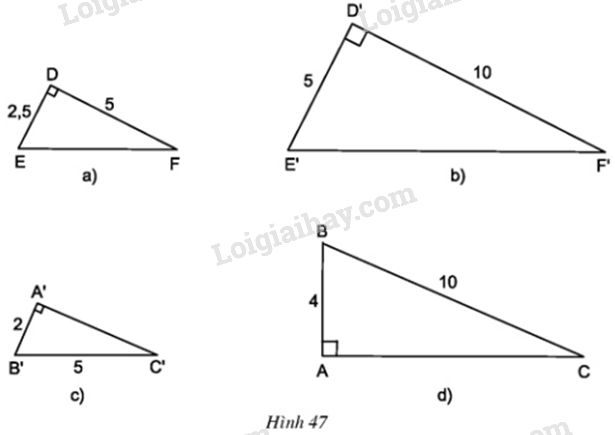
Hãy chỉ ra các cặp tam giác đồng dạng trong hình 47.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Hai tam giác vuông đồng dạng với nhau nếu:
a) Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia
b) Tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia.
Lời giải chi tiết
Xét tam giác \(ΔDEF\) và \(ΔD’E’F’\) có
\(\widehat{EDF}=\widehat{E'D'F'}(=90^0)\)
\(\dfrac{{DE}}{{D'E'}} = \dfrac{{DF}}{{D'F'}} = \dfrac{1}{2}\)
\(⇒ ΔDEF \) đồng dạng \(ΔDE'F'\)( c-g-c)
Áp dụng định lí Py – ta – go vào tam giác vuông \(A'B'C'\) và \(ABC\) ta được:
\(\eqalign{
& A'C{'^2} = B'C{'^2} - A'B{'^2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {5^2} - {2^2} = 21 \cr
& \Rightarrow A'C' = \sqrt {21} \cr
& A{C^2} = B{C^2} - A{B^2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {10^2} - {4^2} = 84 \cr
& \Rightarrow AC = \sqrt {84}=2\sqrt{21} \cr} \)
Xét tam giác \(ABC\) và \(A’B’C’\) có
\(\widehat{BAC}=\widehat{B'A'C'}(=90^0)\)
\(\dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = 2\)
\( \Rightarrow ΔABC\) đồng dạng \(ΔA’B’C’ \) (c-g-c)
