Đề bài
Tìm giá trị nguyên của \(n\) để giá trị của biểu thức \(3{n^3} + 10{n^2} - 5\) chia hết cho giá trị của biểu thức \(3n+1\)
Phương pháp giải - Xem chi tiết
+) Thực hiện phép tính chia như phép chia các số tự nhiên.
+) Sử dụng tính chất phép chia hết.
Lời giải chi tiết
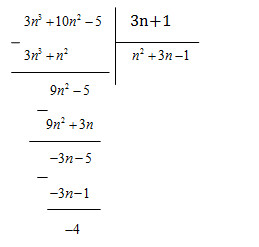
\( \Rightarrow 3{n^3} + 10{n^2} - 5 \)\(= \left( {3n + 1} \right)\left( {{n^2} + 3n - 1} \right) - 4\)
Để phép chia đó là phép chia hết thì \(4 \; \vdots\; (3n + 1) \Rightarrow 3n + 1 \in Ư(4)\)
\(\Rightarrow (3n + 1) \in \left\{ { - 4; - 2; - 1;1;2;4} \right\}\)
\(3n + 1 = - 4 \Rightarrow 3n = - 5 \)\(\Rightarrow n=-\dfrac{5}3 \notin \mathbb{Z}\) (loại)
\(3n + 1 = - 2 \Rightarrow 3n = - 3 \Rightarrow n = - 1\)
\(3n + 1 = - 1 \Rightarrow 3n = - 2 \Rightarrow n =-\dfrac{2}3\notin \mathbb Z\) (loại)
\(3n + 1 = 1 \Rightarrow 3n = 0 \Rightarrow n = 0\)
\(3n + 1 = 2 \Rightarrow 3n = 1 \Rightarrow n =\dfrac{1}3\notin \mathbb Z\) (loại)
\(3n + 1 = 4 \Rightarrow 3n = 3 \Rightarrow n = 1\)
Vậy \(n \in \left\{ { - 1;0;1} \right\}\) thì \(3{n^3} + 10{n^2} - 5\) chia hết cho \(3n+1.\)
soanvan.me
