Đề bài
Cho hình bình hành \(ABCD\). Gọi \(E\) là điểm đối xứng với \(D\) qua điểm \(A\), gọi \(F\) là điểm đối xứng với \(D\) qua điểm \(C\). Chứng minh rằng điểm \(E\) đối xứng với điểm \(F\) qua điểm \(B\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng:
+) Hình bình hành có các cặp cạnh đối song song và bằng nhau.
+) Hai điểm gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.
+) Tiên đề ơclit: Qua một điểm ở ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Lời giải chi tiết
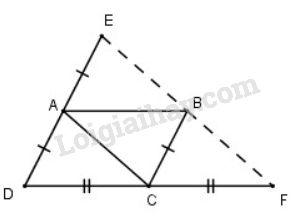
Vì \(ABCD \) là hình bình hành (giả thiết)
\( \Rightarrow A{\rm{D}}//BC, A{\rm{B}}//DC,\)\( A{\rm{D}}=BC, A{\rm{B}}=DC \) (tính chất hình bình hành)
Mà \(E \in A{\rm{D}}\) (giả thiết) \( \Rightarrow AE//BC\)
Vì \(E\) là điểm đối xứng với \(D\) qua điểm \(A\) (giả thiết)
\( \Rightarrow AE = A{\rm{D}}\) (tính chất hai điểm đối xứng qua 1 điểm)
\( \Rightarrow \) \(AE = BC\) (cùng bằng \(AD\))
Kết hợp với \(AE//BC\) (chứng minh trên)
\( \Rightarrow \) Tứ giác \(ACBE\) là hình bình hành (dấu hiệu nhận biết hình bình hành).
\( \Rightarrow \) \(BE // AC, BE = AC\) (1) (tính chất hình bình hành)
Ta có: \(AB//DC\) (chứng minh trên) \(\Rightarrow AB//CF\)
Vì \(F\) là điểm đối xứng với \(D\) qua điểm \(C\) (giả thiết)
\( \Rightarrow CD = CF\) (tính chất hai điểm đối xứng qua 1 điểm)
\( \Rightarrow AB = CF\) (cùng bằng \(DC\))
Kết hợp với \(AB//CF\) (chứng minh trên)
\( \Rightarrow \) Tứ giác \(ACFB\) là hình bình hành (dấu hiệu nhận biết hình bình hành).
\( \Rightarrow \) \(BF // AC, BF = AC\) (2) (tính chất hình bình hành)
Từ (1) và (2) suy ra \(BE\) và \(BF\) cùng song song với \(AC\) và cùng đi qua điểm \(B\) nên theo tiên đề Ơclit \(BE\) trùng \(BF\) hay \(B, E, F\) thẳng hàng.
Lại có: \(BE\) = \(BF\) (cùng bằng \(AC\)) do đó \(B\) là trung điểm của \(EF\)
Vậy \(E\) đối xứng với \(F\) qua \(B\).
soanvan.me
