Video hướng dẫn giải
Các câu sau đúng hay sai ?
LG a.
Tâm đối xứng của một đường thẳng là điểm bất kì của đường thẳng đó.
Phương pháp giải:
Áp dụng định nghĩa: Hình có tâm đối xứng
Điểm \(O\) gọi là tâm đối xứng qua hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua điểm \(O\) cũng thuộc hình \(H.\)
Lời giải chi tiết:
Đúng, vì nếu lấy một điểm \(O\) bất kì trên đường thẳng thì nó chia đường thẳng đó thành hai tia và với bất kì một điểm \(M\), trên tia này cũng luôn có một điểm \(M'\) đối xứng với nó qua \(O\) trên tia kia.
LG b.
Trọng tâm của một tam giác là tâm đối xứng của tam giác đó.
Phương pháp giải:
Áp dụng định nghĩa: Hình có tâm đối xứng
Điểm \(O\) gọi là tâm đối xứng qua hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua điểm \(O\) cũng thuộc hình \(H.\)
Lời giải chi tiết:
Sai, vì nếu lấy điểm đối xứng của 1 đỉnh bất kì của tam giác qua trọng tâm thì điểm đối xứng này không thuộc tam giác.
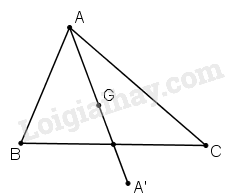
Giả sử tam giác \(ABC\) có trọng tâm \(G.\)
Khi đó điểm \(A’\) đối xứng với \(A\) qua \(G\) không thuộc tam giác.
LG c.
Hai tam giác đối xứng với nhau qua một điểm thì có chu vi bằng nhau.
Phương pháp giải:
Áp dụng định nghĩa: Hình có tâm đối xứng
Điểm \(O\) gọi là tâm đối xứng qua hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua điểm \(O\) cũng thuộc hình \(H.\)
Lời giải chi tiết:
Đúng, vì hai tam giác đối xứng với nhau qua một điểm thì chúng bằng nhau và hai tam giác bằng nhau có chu vi bằng nhau.
soanvan.me
