Đề bài
Cho góc vuông \(xOy\), điểm \(A\) nằm trong góc đó. Gọi \(B\) là điểm đối xứng với \(A\) qua \(Ox\), gọi \(C\) là điểm đối xứng với \(A\) qua \(Oy\). Chứng minh rằng điểm \(B\) đối xứng với điểm \(C\) qua \(O\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Hai điểm \(A\) và \(A'\) gọi là đối xứng nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của \(AA'\)
Chứng minh \(B\) đối xứng với điểm \(C\) qua \(O\) tức là chứng minh \(O\) là trung điểm của \(BC\)
Lời giải chi tiết
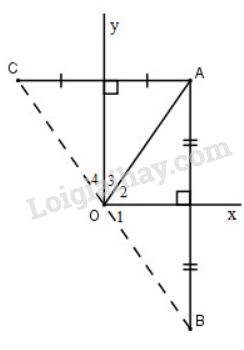
\(A\) đối xứng với \(B\) qua \(Ox\) (giả thiết) nên \(Ox\) là đường trung trực của \(AB\)
\( \Rightarrow \) \(OA = OB\) (tính chất đường trung trực của đoạn thẳng) (1)
\(\Rightarrow \Delta AOB\) cân tại \(O\) (dấu hiệu nhận biết tam giác cân)
Do đó \(Ox\) vừa là đường trung trực đồng thời là phân giác của \( \Delta AOB\)
\( \Rightarrow \) \(\widehat O_1=\widehat O_2\) (3)
\(A\) đối xứng với \(C\) qua \(Oy\) (giả thiết) nên \(Oy\) là đường trung trực của \(AC\)
\( \Rightarrow \) \(OA = OC\) (tính chất đường trung trực của đoạn thẳng) (2)
\(\Rightarrow \Delta AOC\) cân tại \(O\) (dấu hiệu nhận biết tam giác cân)
Do đó \(Oy\) vừa là đường trung trực đồng thời là phân giác của \( \Delta AOC\)
\( \Rightarrow \) \(\widehat O_3=\widehat O_4\) (4)
Từ (3) và (4) \( \Rightarrow \) \(\widehat O_1+\widehat O_2+\widehat O_3+\widehat O_4\)\(=2\widehat O_2+2\widehat O_3=2(\widehat O_2+\widehat O_3)\)\(=2\widehat {xOy}=2.90^0=180^0\)
Do đó \(B, O, C\) thẳng hàng (**)
Từ (1) và (2) \( \Rightarrow \) \(OB = OC\) (*)
Từ (*) và (**) \( \Rightarrow \) \(B\) đối xứng với \(C\) qua \(O\).
soanvan.me
