Video hướng dẫn giải
Một cái lều ở trại hè có dạng lăng trụ đứng tam giác (với các kích thước trên hình 146).
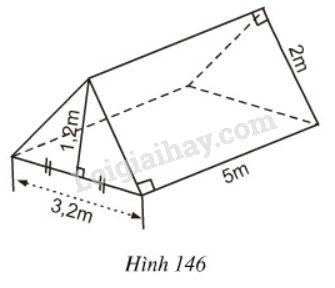
LG a.
Tính thể tích khoảng không ở bên trong lều.
Phương pháp giải:
Áp dụng công thức tính thể tích của hình lăng trụ đứng tam giác.
Giải chi tiết:
Lều là lăng trụ đứng tam giác.
Diện tích đáy (tam giác):
\(S = \dfrac{1}{2}.3,2.1,2 = 1,92\left( {{m^2}} \right)\)
Thể tích khoảng không bên trong lều là:
\(V = Sh = 1,92. 5 = 9,6 (m^3)\)
LG b.
Số vải bạt cần có để dựng lều đó là bao nhiêu?
(Không tính các mép và nếp gấp của lều).
Phương pháp giải:
Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần của hình lăng trụ.
Giải chi tiết:
Số vải bạt cần có để dựng lều chính là diện tích toàn phần của lăng trụ trừ đi diện tích mặt bên có kích thước là \(5\,m\) và \(3,2\,m\).
Diện tích xung quanh lăng trụ là:
\({S_{xq}}= 2ph = (2 + 2+ 3,2) .5 = 36 (m^2)\)
Diện tích toàn phần:
\({S_{tp}} = {S_{xq}} + 2{S_đ}= 36 + 2.1,92 \)\(\,= 39,84 (m^2)\)
Diện tích mặt bên kích thước \(5\,m\) và \(3,2\,m\) là:
\(S = 5.3,2 = 16 (m^2)\)
Vậy số vải bạt cần có để dựng lều là:
\(39,84 - 16 = 23,84 (m^2)\)
Chú ý:Có thể tính bằng cách khác là tổng diện tích hai mặt bên và hai đáy.
soanvan.me
