Đề bài
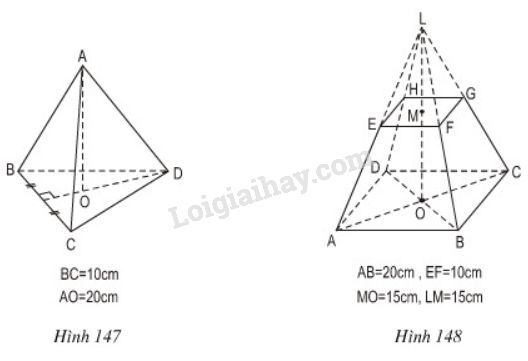
Tính thể tích của hình chóp đều, hình chóp cụt đều sau đây (h.147 và h.148)
Hướng dẫn: Hình chóp \(L.EFGH\) cũng là hình chóp đều
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính thể tích của hình chóp đều.
\(V = \dfrac{1}{3}Sh\)
Trong đó: \(S\) là diện tích đáy hình chóp.
\(h\) là chiều cao hình chóp.
Lời giải chi tiết
a) Hình 147
Chiều cao của tam giác đều BCD cạnh 10 cm là:
\(DH =\sqrt{AC^2-\left(\dfrac{BC}{2}\right)^2}=\sqrt{10^2-5^2}\)\(= 5\sqrt 3 \approx 8,65\) \(\left( {cm} \right)\)
Diện tích đáy của hình chóp là:
\(S = \dfrac{1}{2}.BC.DH = \dfrac{1}{2}.10.8,65 \)\(\,= 43,25\left( {c{m^2}} \right)\)
Thể tích hình chóp đều:
\(V = \dfrac{1}{3}.S.h = \dfrac{1}{3}.43,25.20 = 288,33\) \((c{m^3})\)
b) Hình 148
Thể tích của hình chóp cụt đều chính là hiệu của thể tích hình chóp đều \(L.ABCD\) với thể tích của hình chóp đều \(L.EFGH\). Do có: \(LO = LM + MO = 15 + 15 \)\(\,= 30\, (cm)\)
+ Tính thể tích hình chóp đều \(L.ABCD\):
- Diện tích đáy: \(S_1 = AB^2= 20^2= 400 (cm^2)\)
- Thể tích hình chóp đều \(L.ABCD\) là:
\({V_1} = \dfrac{1}{3}{S_1}{h_1} = \dfrac{1}{3}.400.30 \)\(\,= 4000\left( {c{m^3}} \right)\)
+Thể tích hình chóp đều \(L.EFGH\):
-Diện tích đáy: \(S_2 = E{F^2} = {10^2} = 100(c{m^2})\)
-Thể tích hình chóp đều \(L.EFGH\) là:
\({V_2} = \dfrac{1}{3}{S_2}{h_2} = \dfrac{1}{3}.100.15 = 500\left( {c{m^3}} \right)\)
Vậy thể tích hình chóp cụt đều là:
\(V = {V_1} - {V_2} = 4000 - 500 \)\(\,= 3500(c{m^3})\)
soanvan.me
