LG a
Khảo sát sự biến thiên và vẽ đồ thị \((C)\) của hàm số \(y = {{{x^2}} \over {x + 1}}\)
Lời giải chi tiết:
\(D = R\backslash \left\{ { - 1} \right\}\)
\(\eqalign{
& y' = {{{x^2} + 2x} \over {{{\left( {x + 1} \right)}^2}}} \cr
& y' = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = - 2 \hfill \cr} \right. \cr} \)
Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {0; + \infty } \right)\)
Hàm số nghịch biến trên khoảng \((-2;-1)\) và \((1;0)\)
Hàm số đạt cực đại tại \(x=-2\), \(y_{CĐ}=-4\)
Hàm số đạt cực tiểu tại \(x=0\) , \(y_{CT}=0\)
\(\mathop {\lim }\limits_{x \to - {1^ + }} y = + \infty \)
\(\mathop {\lim }\limits_{x \to - {1^ - }} y = - \infty \)
Vậy \(x=-1\) là tiệm cận đứng.
Ta có: \(y = \frac{{{x^2}}}{{x + 1}} = \frac{{{x^2} - 1 + 1}}{{x + 1}} \) \(= \frac{{{x^2} - 1}}{{x + 1}} + \frac{1}{{x + 1}} = x - 1 + \frac{1}{{x + 1}}\)
\(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - (x - 1)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } \left( {{1 \over {x + 1}}} \right) = 0\)
Vậy \(y=x-1\) là tiệm cận xiên.
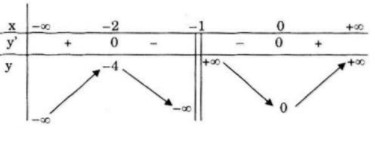
Bảng biến thiên
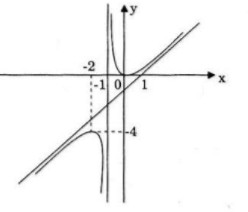
Đồ thị
Đồ thị giao \(Ox\), \(Oy\) tại \(O(0;0)\)
\(x=-2\rightarrow y=-4\)
LG b
Từ đồ thị \((C)\) suy ra cách vẽ đồ thị của hàm số \(y = {{{x^2}} \over {\left| {x + 1} \right|}}\)
Lời giải chi tiết:
Ta có
\(y = {{{x^2}} \over {\left| {x + 1} \right|}} = \left\{ \matrix{
{{{x^2}} \over {x + 1}}\,\,\text{nếu} \,x > - 1 \hfill \cr
- {{{x^2}} \over {x + 1}}\,\,\text{ nếu }\,x < - 1 \hfill \cr} \right.\)
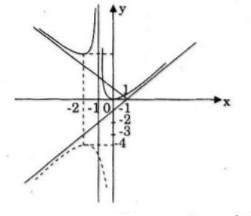
Do đó cách dựng:
- Giữ nguyên phần đồ thị \((C)\) ở bên phải tiệm cận đứng \(x = -1\)
- Lấy đối xứng của phần \((C)\) bên trái tiệm cận đứng qua trục hoành.
- Hợp hai phần đồ thị này ta được đồ thị hàm số cần tìm.
soanvan.me
