Đề bài
Trong mặt phẳng, cho đa giác\({A_1}{A_2}{A_3}...{A_n}\) có n cạnh \((n \ge 3)\). Gọi \({S_n}\) là tổng số đo các góc trong của đa giác.
a) Tính \({S_3},{S_4},{S_5}\) tương ứng với trường hợp đa giác là tam giác, tứ giác, ngũ giác.
b) Từ đó, dự đoán công thức tính \({S_n}\) và chứng minh công thức đó bằng phương pháp quy nạp toán học.
Lời giải chi tiết
a)
\(\begin{array}{l}{S_3} = {180^ \circ }\\{S_4} = {180^ \circ } + {180^ \circ } = {2.180^ \circ }\\{S_5} = {2.180^ \circ } + {180^ \circ } = {3.180^ \circ }\end{array}\)
b) Dự đoán \({S_n} = (n - 2){.180^ \circ }\) với mọi \(n \ge 3\).
Ta chứng minh công thức bằng phương pháp quy nạp
Với \(n = 3\) ta có \({S_3} = {180^ \circ }\)
Vậy công thức đúng với \(n = 3\)
Giả sử công thức đúng với \(n = k\) nghĩa là có \({S_k} = (k - 2){.180^ \circ }\)
Ta chứng minh công thức đúng với \(n = k + 1\) tức là chứng minh \({S_{k + 1}} = (k - 1){.180^ \circ }\)
Thật vậy, ta có
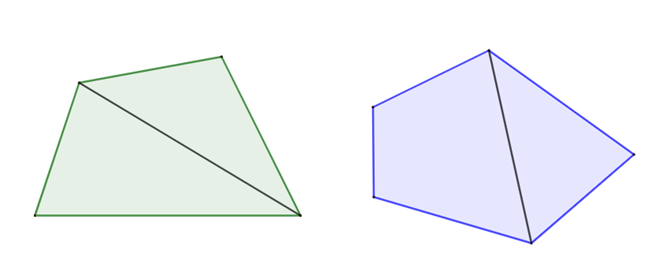
Xét đa giác k+1 cạnh: \({A_1}{A_2}{A_3}...{A_k}{A_{k + 1}}\). Kẻ đường chéo \({A_1}{A_k}\), chia đa giác này thành đa giác \({A_1}{A_2}{A_3}...{A_k}\) k cạnh và tam giác \({A_1}{A_k}{A_{k + 1}}\). Khi đó tổng các góc trong của đa giác k+1 cạnh \({A_1}{A_2}{A_3}...{A_k}{A_{k + 1}}\) bằng tổng các góc trong cả đa giác k cạnh \({A_1}{A_2}{A_3}...{A_k}\) và tam giác \({A_1}{A_k}{A_{k + 1}}\)
Do đó: \({S_{k + 1}} = {S_k} + {S_3} = (k - 2){.180^ \circ } + {180^ \circ } = (k - 1){.180^ \circ }\)
Vậy công thức đúng với mọi số tự nhiên \(n \ge 3\).
