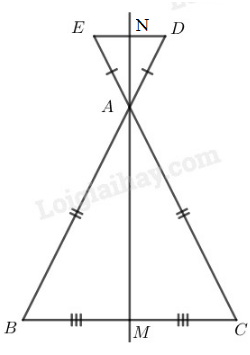
Đề bài
Cho tam giác \(ABC\) cân tại \(A.\) Trên tia đối của tia \(AB\) lấy điểm \(D,\) trên tia đối của tia \(AC\) lấy điểm \(E\) sao cho \(AD = AE.\) Gọi \(M\) là trung điểm của \(BC.\) Chứng minh rằng \(D\) đối xứng với \(E\) qua \(AM.\)
Phương pháp giải - Xem chi tiết
+) Trong tam giác cân, đường trung tuyến ứng với cạnh đáy cũng là đường trung trực, đường phân giác.
+) Sử dụng định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
Lời giải chi tiết
\(∆ ABC\) cân tại \(A\) có \(AM\) là đường trung tuyến
\(⇒ AM\) là tia phân giác \(\widehat {BAC}\) (tính chất tam giác cân)
\( \Rightarrow \widehat {BAM} = \widehat {MAC}\) \((1)\)
Kéo dài \(MA\) cắt \(DE\) tại \(N\), ta có:
\(\widehat {BAM} = \widehat {DAN}\) (đối đỉnh) \((2)\)
\(\widehat {MAC} = \widehat {NAE}\) (đối đỉnh) \((3)\)
Từ \((1),\) \((2)\) và \((3)\) suy ra: \(\widehat {DAN} = \widehat {NAE}\)
Hay \(AN\) là tia phân giác của góc DAE.
\(∆ ADE\) cân tại \(A\) có \(AN\) là tia phân giác
\(⇒ AN\) là đường trung trực của \(DE\)
hay \(AM\) là đường trung trực của \(DE\)
Vậy \(D\) đối xứng với \(E\) qua \(AM.\)
soanvan.me