Đề bài
Tam giác \(ABC\) có \(AB < AC.\) Gọi \(d\) là đường trung trực của \(BC.\) Vẽ điểm \(K\) đối xứng với điểm \(A\) qua đường thẳng \(d.\)
\(a)\) Tìm các đoạn thẳng đối xứng với đoạn thẳng \(AB\) qua \(d,\) đối xứng với đoạn thẳng \(AC\) qua \(d.\)
\(b)\) Tứ giác \(AKCB\) là hình gì \(?\) Vì sao \(?\)
Phương pháp giải - Xem chi tiết
+) Sử dụng định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
+) Sử dụng định nghĩa: Hình thang là tứ giác có hai cạnh đối song song.
+) Hình thang có hai đường chéo bằng nhau là hình thang cân.
+) Nếu hai đoạn thẳng đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
Lời giải chi tiết
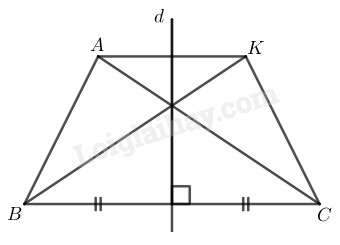
\(a)\) \(d\) là đường trung trực của \(BC\) nên \(B\) và \(C\) đối xứng qua \(d\)
\(K\) đối xứng với \(A\) qua \(d\)
Do đó:
Đoạn thẳng đối xứng với đoạn \(AB\) qua \(d\) là đoạn \(KC\)
Đoạn thẳng đối xứng với đoạn \(AC\) qua \(d\) là đoạn \(KB\)
\(b)\) \(d\) là đường trung trực của \(BC\;\; (gt)\)
\( ⇒ d ⊥ BC\)
\(A\) và \(K\) đối xứng qua \(d\) nên \(d\) là trung trực của \(AK\)
\(⇒ d ⊥ AK\)
Suy ra: \(BC // AK.\) Tứ giác \(ABCK\) là hình thang
\(AC\) và \(KB\) đối xứng qua \(d\) nên \(AC = BK.\)
Vậy hình thang \(ABCK\) là hình thang cân.
soanvan.me
