Xét chiều biến thiên và tìm cực trị (nếu có) của các hàm số sau:
LG a
\(y = \sqrt {3x + 1} \)
Lời giải chi tiết:
TXĐ: \(D = \left[ { - {1 \over 3}; + \infty } \right)\)
\(y' = {3 \over {2\sqrt {3x + 1} }} > 0\,\forall x > - {1 \over 3}\)
Hàm số đồng biến \(\left( { - {1 \over 3}; + \infty } \right)\), hàm số không có cực trị.
LG b
\(y = \sqrt {4x - {x^2}} \)
Lời giải chi tiết:
ĐK: \(4x - {x^2} \ge 0 \Leftrightarrow 0 \le x \le 4\)
TXĐ: \(D = \left[ {0;4} \right]\)
\(y' = {{4 - 2x} \over {2\sqrt {4x - {x^2}} }}\), \(\forall x \in \left( {0;4} \right)\)
\(y' = 0 \Leftrightarrow x = 2;\,y\left( 2 \right) = 2\)
Bảng biến thiên
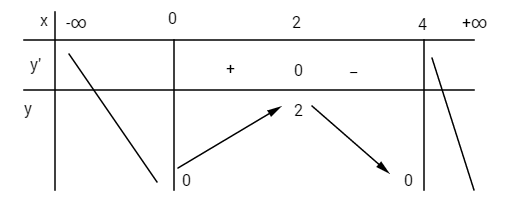
Hàm số đạt cực đại tại điểm \(x = 2\); giá trị cực đại \(y(2) = 2\).
LG c
\(y = x + \sqrt x \)
Lời giải chi tiết:
TXĐ: \(D = \left[ {0; + \infty } \right)\)
\(y' = 1 + {1 \over {2\sqrt x }} > 0,\,\forall x > 0\)
Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\), hàm số không có cực trị.
LG d
\(y = x - \sqrt x \)
Lời giải chi tiết:
TXĐ: \(D = \left[ {0; + \infty } \right)\)
\( y' = 1 - {1 \over {2\sqrt x }} \), \(\forall x \in \left( {0; + \infty } \right)\)
\(y' = 0 \)\( \Leftrightarrow 1 - \frac{1}{{2\sqrt x }} = 0\)
\( \Leftrightarrow \frac{{2\sqrt x - 1}}{{2\sqrt x }} = 0 \Leftrightarrow 2\sqrt x - 1 = 0\) \( \Leftrightarrow \sqrt x = \frac{1}{2} \Leftrightarrow x = \frac{1}{4}\)
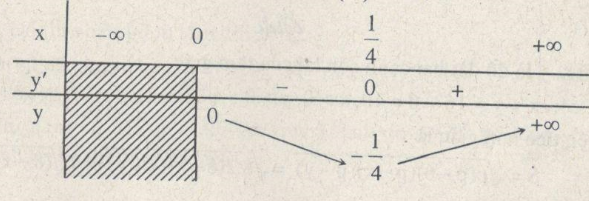
Hàm số đạt cực tiểu tại điểm \(x = {1 \over 4}\); giá trị cực tiểu \(y\left( {{1 \over 4}} \right) = - {1 \over 4}\)
soanvan.me
