Đề bài
Chứng minh \(\root 3 \of {7 + 5\sqrt 2 } + \root 3 \of {7 - 5\sqrt 2 } = 2\)
Lời giải chi tiết
Đặt \(x = \root 3 \of {7 + 5\sqrt 2 } + \root 3 \of {7 - 5\sqrt 2 } \)
Ta có:
\({x^3} = \left( {\root 3 \of {7 + 5\sqrt 2 } + \root 3 \of {7 - 5\sqrt 2 } } \right)^3\)
\( = 7 + 5\sqrt 2 + 7 - 5\sqrt 2 \) \(+ 3\root 3 \of {{{\left( {7 + 5\sqrt 2 } \right)}^2}} .\root 3 \of {7 - 5\sqrt 2 } \) \(+ 3\root 3 \of {7 + 5\sqrt 2 } .\root 3 \of {{{\left( {7 - 5\sqrt 2 } \right)}^2}} \)
\(= 14 + 3\sqrt[3]{{\left( {7 + 5\sqrt 2 } \right)\left( {7 - 5\sqrt 2 } \right)}}.\)\(.\left( {\sqrt[3]{{7 + 5\sqrt 2 }} + \sqrt[3]{{7 - 5\sqrt 2 }}} \right)\)
\( = 14 - 3\left( {\root 3 \of {7 + 5\sqrt 2 } + \root 3 \of {7 - 5\sqrt 2 } } \right) \)
\(= 14 - 3x\).
Từ đó suy ra: \({x^3} + 3x - 14 = 0\,\,\,\,\left( 1 \right)\)
\(\left( 1 \right) \Leftrightarrow \left( {x - 2} \right)\left( {{x^2} + 2x + 7} \right) = 0 \)
\(\Leftrightarrow x - 2 = 0 \Leftrightarrow x = 2\)
(vì \({x^2} + 2x + 7 > 0\))
Vậy \(\root 3 \of {7 + 5\sqrt 2 } + \root 3 \of {7 - 5\sqrt 2 } = 2\)
Cách khác:
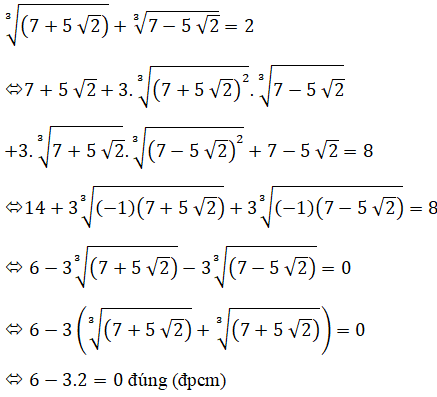
soanvan.me
