Đề bài
Cho tam giác ABC, trong đó \(BC = 20cm,\widehat {ABC} = {22^o},\widehat {ACB} = {30^o}\).
a) Tính khoảng cách từ điểm B đến đường thẳng AC.
b) Tính khoảng cách từ điểm A đến đường thẳng BC.
c) Tính các cạnh và góc còn lại của tam giác ABC.
Phương pháp giải - Xem chi tiết
Sử dụng các hệ thức về cạnh và góc trong tam giác vuông và định lý tổng 3 góc trong tam giác để tính.
Lời giải chi tiết
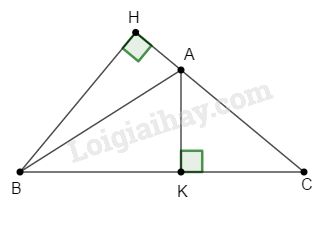
a) Tính khoảng cách từ điểm B đến đường thẳng AC.
Gọi khoảng cách từ điểm B đến đường thẳng AC là BH
Xét tam giác BHC vuông tại H: \(BH = BC.\sin \widehat {ACB} = 20.\sin {30^o} = 10\,\,(cm)\)
b) Tính khoảng cách từ điểm A đến đường thẳng BC.
Xét tam giác BHC vuông tại H \( \Rightarrow \widehat {HBC} = {90^o} - \widehat {ACB} = {60^o}\)
\( \Rightarrow \widehat {HBA} = \widehat {HBC} - \widehat {ABC} = {60^o} - {22^o} = {38^o}\)
Xét tam giác BHA vuông tại H: \(BH = BA.\cos \widehat {HBA}\)
\(\Rightarrow BA = \dfrac{{BH}}{{\cos \widehat {HBA}}} = \dfrac{{10}}{{\cos {{38}^o}}}\,\,(cm)\)
Gọi khoảng cách từ điểm A đến đường thẳng BC là AK
Xét tam giácAKB vuông tại K: \(AK = BA.\sin \widehat {ABC}\)\(\, = \dfrac{{10}}{{\cos {{38}^o}}}.\sin {22^o} \approx 4,75\,\,(cm)\)
c) Tính các cạnh và góc còn lại của tam giác ABC.
Xét tam giácAKC vuông tại K: \(AK = AC.\sin \widehat {ACB} \) \(\Rightarrow AC = \dfrac{{AK}}{{\sin \widehat {ACB}}} \approx 9,51\,\,(cm)\)
Xét tam giác ABC có:
\(\widehat {BAC} = {180^o} - \widehat {ABC} - \widehat {ACB}\)\(\, = {180^o} - {22^o} - {30^o} = {128^o}\)(định lý tổng 3 góc trong tam giác)
soanvan.me
