Đề bài
Cho hình lăng trụ tam giác \(ABC.A'B'C'\) có \(\overrightarrow{AA'}\) = \(\overrightarrow{a}\), \(\overrightarrow{AB}\) = \(\overrightarrow{b}\), \(\overrightarrow{AC}\) = \(\overrightarrow{c}\). Hãy phân tích (hay biểu thị véctơ \(\overrightarrow{B'C}\), \(\overrightarrow{BC'}\) qua các véctơ \(\overrightarrow{a}\),\(\overrightarrow{b}\), \(\overrightarrow{c}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Xen điểm thích hợp để làm xuất hiện các véc tơ \(\overrightarrow{a}\),\(\overrightarrow{b}\), \(\overrightarrow{c}\), sử dụng các cặp vecto bằng nhau và bằng các vecto đã cho.
Lời giải chi tiết
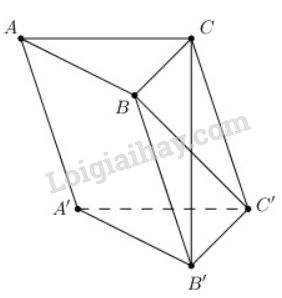
\(\eqalign{& \overrightarrow {B'C} = \overrightarrow {B'A'} + \overrightarrow {A'A} + \overrightarrow {AC} \cr &= - \overrightarrow {AB} - \overrightarrow {AA'} + \overrightarrow {AC} \cr &= - \overrightarrow b - \overrightarrow a + \overrightarrow c \cr & \overrightarrow {BC'} = \overrightarrow {BA} + \overrightarrow {AA'} + \overrightarrow {A'C'} \cr & = - \overrightarrow {AB} + \overrightarrow {AA'} + \overrightarrow {AC} \cr &= - \overrightarrow b + \overrightarrow a + \overrightarrow c \cr} \)
Nhận xét: Ba véctơ \(\overrightarrow{a}; \overrightarrow{b}; \overrightarrow{c}\) ở trên gọi là bộ ba véctơ cơ sở (dùng để phân tích các véctơ khác).
Cách khác:
\(\begin{array}{l}
\overrightarrow {B'C} = \overrightarrow {AC} - \overrightarrow {AB'} \\
= \overrightarrow {AC} - \left( {\overrightarrow {AB} + \overrightarrow {BB'} } \right)\\
= \overrightarrow {AC} - \overrightarrow {AB} - \overrightarrow {BB'} \\
= \overrightarrow {AC} - \overrightarrow {AB} - \overrightarrow {AA'} \\
= \overrightarrow c - \overrightarrow b - \overrightarrow a \\
\overrightarrow {BC'} = \overrightarrow {AC'} - \overrightarrow {AB} \\
= \overrightarrow {AA'} + \overrightarrow {A'C'} - \overrightarrow {AB} \\
= \overrightarrow {AA'} + \overrightarrow {AC} - \overrightarrow {AB} \\
= \overrightarrow a + \overrightarrow c - \overrightarrow b
\end{array}\)
soanvan.me
