Đề bài
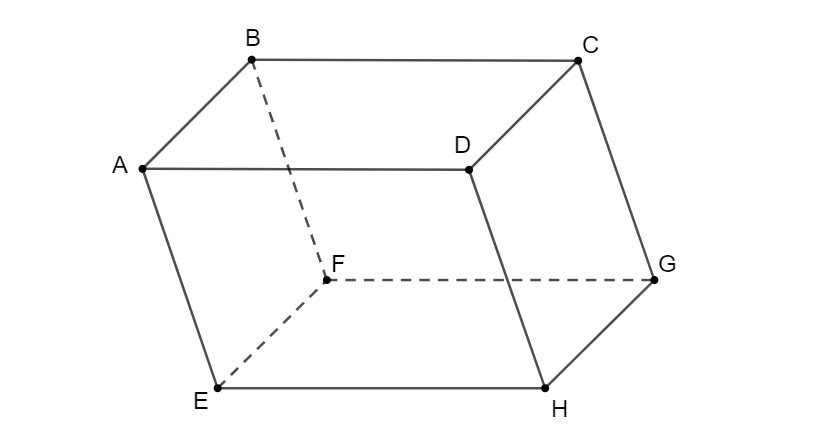
Cho hình hộp ABCD.EFGH. Hãy thực hiện các phép toán sau đây (h.3.2):
\(\eqalign{
& a)\,\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {{\rm{EF}}} + \overrightarrow {GH} \cr
& b)\,\overrightarrow {BE} - \overrightarrow {CH} \cr} \)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng các quan hệ véc tơ bằng nhau, đối nhau để tính toán.
Lời giải chi tiết
\(\eqalign{
& a)AB = CD \Rightarrow \overrightarrow {CD} = - \overrightarrow {AB} \cr
& {\rm{EF}}\,{\rm{ = }}\,{\rm{GH}} \Rightarrow \,\overrightarrow {GH} = - \overrightarrow {{\rm{EF}}} \cr &\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {{\rm{EF}}} + \overrightarrow {GH} \cr
& = \overrightarrow {AB} - \overrightarrow {AB} + \overrightarrow {{\rm{EF}}} - \overrightarrow {{\rm{EF}}} \cr &= \overrightarrow 0 - \overrightarrow 0 = \overrightarrow 0 \cr } \)
b) Tứ giác \(BCHE\) có:
\(BC=EH\) và \(BC//EH\) nên là hình bình hành.
\( \Rightarrow \overrightarrow {BE} = \overrightarrow {CH} \Rightarrow \overrightarrow {BE} - \overrightarrow {CH} = \overrightarrow 0 \)
soanvan.me