Đề bài
Chứng minh rằng các phép tịnh tiến, đối xứng trục, đối xứng tâm là những phép dời hình.
Lời giải chi tiết
* Phép tịnh tiến
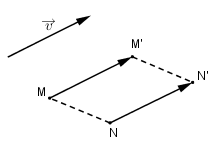
Giả sử \({T_{\overrightarrow v }}\) là phép tịnh tiến theo vectơ \(\overrightarrow v \)
\(\eqalign{
& {T_{\overrightarrow v }}:\,M \to M' \cr
& \,\,\,\,\,\,\,\,N \to N' \cr} \)
Ta có \(\overrightarrow {MM'} = \overrightarrow {NN'} = \overrightarrow v\) nên MM'N'N là hình bình hành
\( \Rightarrow \overrightarrow {MN} = \overrightarrow {M'N'} \Rightarrow MN = M'N'\)
Vậy phép tịnh tiến là một phép dời hình.
* Phép đối xứng trục
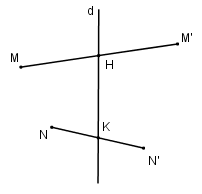
Giả sử \({\tilde N_d}\) là phép đối xứng qua đường thẳng \(d\)
Giả sử
\({{\tilde N}_d}:M \to M'\)
\(N \to N'\)
Gọi \(H\) và \(K\) lần lượt là trung điểm của \(MM’\) và \(NN’\).
Ta có:
\(\eqalign{
& \overrightarrow {MN} + \overrightarrow {M'N'}\cr & = \left( {\overrightarrow {MH} + \overrightarrow {HK} + \overrightarrow {KN} } \right) \cr & + \left( {\overrightarrow {M'H} + \overrightarrow {HK} + \overrightarrow {KN'} } \right) \cr & = \left( {\overrightarrow {MH} + \overrightarrow {M'H} } \right) + \left( {\overrightarrow {KN} + \overrightarrow {KN'} } \right) \cr & + \left( {\overrightarrow {HK} + \overrightarrow {HK} } \right) \cr & = \overrightarrow 0 + \overrightarrow 0 + 2\overrightarrow {HK} \cr &= 2\overrightarrow {HK} \cr
& \overrightarrow {MN} - \overrightarrow {M'N'}\cr & = (\overrightarrow {HN} - \overrightarrow {HM} )- ( \overrightarrow {HN'} - \overrightarrow {HM'} )\cr & = \left( {\overrightarrow {HN} - \overrightarrow {HN'} } \right) + \left( {\overrightarrow {HM'} - \overrightarrow {HM} } \right)\cr &= \overrightarrow {N'N} + \overrightarrow {MM'} \cr} \)
Vì \(\overrightarrow {MM'} \bot \overrightarrow {HK} \) và \(\overrightarrow {N'N} \bot \overrightarrow {HK} \) nên
\(\eqalign{
& {\overrightarrow {MN} ^2} - {\overrightarrow {M'N'} ^2} \cr &= \left( {\overrightarrow {MN} + \overrightarrow {M'N'} } \right)\left( {\overrightarrow {MN} - \overrightarrow {M'N'} } \right) \cr &= 2\overrightarrow {HK} \left( {\overrightarrow {N'N} + \overrightarrow {MM'} } \right) \cr &= 2\overrightarrow {HK} .\overrightarrow {N'N} + 2\overrightarrow {HK} .\overrightarrow {MM'} \cr &= 2.0 + 2.0 = 0 \cr
& \Rightarrow M{N^2} = M'N{'^2} \Rightarrow MN = M'N' \cr} \)
Vậy phép đối xứng qua \(d\) là phép dời hình.
Cách khác:
Giả sử phép đối xứng qua đường thẳng d biến M thành M’, N thành N’
Gọi (P) là mặt phẳng chứa NM’ và (P) // MM’
\({M_1},{M_1}'\) lần lượt là hình chiếu của M, M’ trên (P); O = ∩(P).
Ta có d ⊥ (P) nên O đồng thời là trung điểm của \({M_1}{M_1}'\) và NN'.
Vậy phép đối xứng tâm O biến \(M_1\) thành \(M_1'\), N thành N’ nên \({M_1},{M_1}'\) nên \(M_1 N=M_1'N'\).
Mặt khác \(M_1 N,M_1'N'\) lần lượt là hình chiếu của MN, M’N’ trên (P), MM’ // (P) nên MN = M’N’.
Vậy phép đối xứng qua đường thẳng là phép dời hình.
* Phép đối xứng tâm
Nếu phép đối xứng qua tâm \(O\) biến hai điểm \(M, N\) lần lượt thành hai điểm \(M’, N’\) thì \(\overrightarrow {OM'} = - \overrightarrow {OM} ;\overrightarrow {ON'} = - \overrightarrow {ON} \)
suy ra \(\overrightarrow {M'N'} = \overrightarrow {ON'} - \overrightarrow {OM'} \) \( = - \overrightarrow {ON} + \overrightarrow {OM} = \overrightarrow {NM} \) \(\Rightarrow M'N' = MN\)
Vậy phép đối xứng tâm \(O\) là một phép dời hình.
soanvan.me
